Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 63b

Calcular a área entre as curvas:

b) 2 r = 3 e r = 1 + cos theta

Passo 1

A área pedida está na figura:

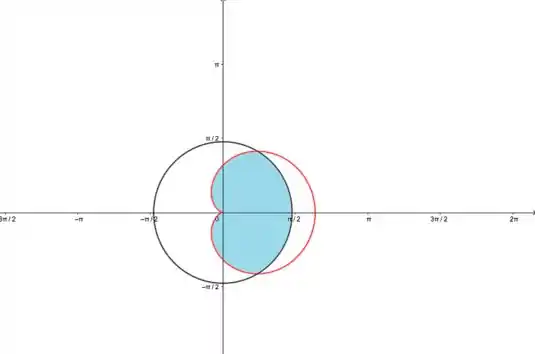
Vamos ver onde ocorre a interseções das funções:

(3)/(2) = 1 + cos theta

cos theta = (3)/(2) - 1

cos theta = (1)/(2)

theta = (pi)/(3)

Outra coisa que a gente pode se aproveitar é do fato de que a função é simétrica em relação ao eixo x , então a gente pode fazer só a área da parte de cima do eixo, e depois multiplicar por 2.

Passo 2

Mas olha só, no intervalo de [0 , (pi)/(3)] , a gente tem a função r = (3)/(2) e de [(pi)/(3) , pi] (que é onde está o eixo x ) a gente tem a função r = 1 + cos theta .

Ou seja, são áreas diferentes que vamos calcular nesses intervalos.

Vamos primeiro na área do intervalo de [0 , (pi)/(3)] ...

A_1 = (1)/(2) int_0^((pi)/(3)) ((3)/(2))^2 d theta

A_1 = (1)/(2) ((9)/(4)) ((pi)/(3))

A_1 = (9 pi)/(24)

Passo 3

Agora vamos pra área da região de [(pi)/(3) , pi] ...

A_2 = (1)/(2) int_((pi)/(3))^(pi) (1 + cos theta)^2 d theta

= (1)/(2) int_((pi)/(3))^(pi) 1 + 2 cos theta + cos^2 theta d theta

= (1)/(2) [theta + 2 s e n theta + (theta)/(2) + (s e n 2 theta)/(4)]_((pi)/(3))^(pi)

= (1)/(2) [pi + (pi)/(2) - (pi)/(3) - sqrt(3) - (pi)/(6) - sqrt(3)]

= (1)/(2) [pi - (9 sqrt(3))/(8)]

A_2 = (pi)/(2) - (9 sqrt(3))/(16)

Passo 4

Beleza, a soma dessas duas áreas dá a área da parte de cima do gráfico, então pra acharmos a área total, é só a gente fazer:

A = 2 (A_1 + A_2)

A = 2 ((9 pi)/(24) + (pi)/(2) - (9 sqrt(3))/(16))

A = (14 pi - 9 sqrt(3))/(8) u . a

Pronto! Essa é a área pedida😉

Resposta

A = (14 pi - 9 sqrt(3))/(8) u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde
Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde
Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 9. r = 4 - 4 c o s θ
Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 10 . r =3 - 3 s e n θ
Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada 7. (a) r s e n θ = - 4 ; br = - 4 s e n θ