Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 60

Encontrar a área da região do 1 º   quadrante delimitada pelo primeiro laço da espiral r = 2 θ , θ ≥ 0 e pelas retas θ = π 4   e   θ = π 3 .

Passo 1

A área pedida está na figura:

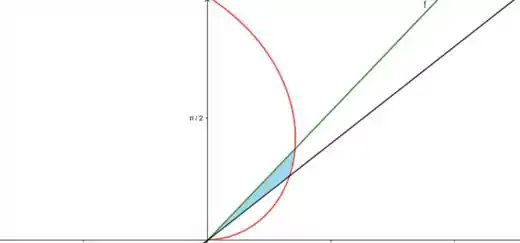
Passo 2

A gente usa a fórmula:

A = 1 2 ∫ α β f θ 2 d θ  

Aí é só a gente aplicar o nosso caso na fórmula...

A = 1 2 ∫ π 4 π 3 2 θ 2 d θ  

A = 1 2 ∫ π 4 π 3 4 θ 2 d θ

A = 1 2 4 θ 3 3 π 4 π 3

A = 1 2 4 π 3 27 3 - 4 π 3 64 3

A = 1 2 4 π 3 81 - 4 π 3 192

A = 1 2 256 π 3 - 108   π 3 5184

A = 1 2 148 π 3 5184

A = 37 π 3 2592   u . a

Prontinho! Essa é a área que pediram😉

Resposta

A = 37 π 3 2592   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 23 a 28, ache a equação polar da cônica que tem um foco na origem e que satisfaz as condições dadas.27. Elipse ; vétices em 3 ,0 e1 , π .
Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde
Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde
Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde
Nos exercícios de 11 a 22, a equação é de uma cônica tendo um foco na origem. Em cada exercício, (a) ache a excentricidade, (b) identifique a cônica, (c) escreva a equação da diretriz que corresponde