Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.2 - Ex. 11

Calcular as integrais curvilíneas.

∫ C ( x + y + z )   d s , onde C   é o quadrado de vértices 1,0 , 1 ,   1,1 , 1 ,   0,1 , 1 ,   ( 0,0 , 1 ) .

Passo 1

Bom, a região é a figura abaixo, sendo que está no plano z = 1 .

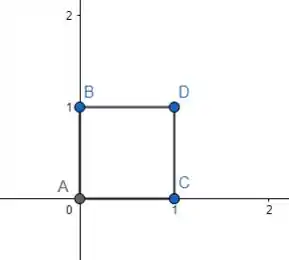
Vamos ter que dividir em 4 integrais de linha, ligando os pontos 2 a 2 e escrevendo a equação das retas de cada uma. Vamos chamar de:

  • C 1 : a   r e t a   q u e   p a s s a   p o r   A   e   C : t , 0,1
  • C 2 : a   r e t a   q u e   p a s s a   p o r   C   e   D : 1 , t , 1
  • C 3 : a   r e t a   q u e   p a s s a   p o r   D   e   B : 1 + t ,   1,1
  • C 4 : a   r e t a   q u e   p a s s a   p o r   B   e   A : ( 0,1 - t , 1 )  

Passo 2

Parametrizações prontas, agora a gente deriva cada uma e faz a norma (que é o nosso d s ):

C 1 ' = 1,0 , 0 → C 1 ' = 1

C 2 ' = 0,1 , 0 → C 2 ' = 1

C 3 ' = 1,0 , 0 → C 3 ' = 1

C 4 ' = 0 , - 1,1 = C 4 ' 1

Beleza, agora a gente monta a integral de linha de cada uma e depois soma...

Passo 3

C 1 : ∫ 0 1 t + 0 + 1 1 d t = ∫ 0 1 t + 1 = t 2 2 + t 0 1 = 1 2 + 1 = 3 2

C 2 : ∫ 0 1 1 + t + 1 1   d t = ∫ 0 1 t + 2   d t = t 2 2 + 2 t 0 1 = 1 2 + 2 = 5 2

C 3 : ∫ 0 1 1 + t + 1 + 1 1 d t = ∫ 0 1 t + 3   d t = t 2 2 + 3 t 0 1 = 1 2 + 3 = 7 2

C 4 : ∫ 0 1 0 + 1 - t + 1 1 d t = ∫ 0 1 2 - t   d t = 2 t - t 2 2 0 1 = 2 - 1 2 = 3 2

Somando tudo agora, a gente tem:

3 2 + 5 2 + 7 2 + 3 2 = 18 2 = 9  

`Prontinho!

Resposta

9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3. Deseja-se construir uma peça de zinco que tem a forma da superfície do cilindro x 2 + y 2 = 4 Compreendida entre os planos z = 0 x + y + z = 2 z ≥ 0 Se o metro quadrado do zinco custa M reais , cal
2. Um arame tem a forma da curva obtida como interseção da porção da esfera x 2 + y 2 + z 2 = 4 y ≥ 0 Com o plano x + z = 2 Sabendo-se que a densidade em cada ponto do arame é dada por f x , y , z = x
4. Calcule ∫ C F ⋅ dr → Ondeh. Fx , y , z = x y , x 2 + z ,y 2 - x e C é a curva de interseção do cone x 2 + y 2 = z 2 ,z0 com o cilindro x = y 2 de 0,0 , 0 a 1,1 , 2
4. Calcule ∫ C F ⋅ dr → Ondeg. Fx , y , z = x 2 - y 2 ,z 2 - x 2 ,y 2 - z 2 e C é a curva de interseção da esfera x 2 + y 2 + z 2 = 4 com o plano y = 1 , percorrida no sentido anti-horario
Encontre a integral de linha de f ( x , y , x ) = 3 / x 2 + y 2 + z 2 sobre a curva r ( t ) = t i + t j + t k , 1 ≤ t ≤ ∞ .