Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 3

3. Deseja-se construir uma peça de zinco que tem a forma da superfície do cilindro

x 2 + y 2 = 4

Compreendida entre os planos

z = 0

x + y + z = 2

z ≥ 0

Se o metro quadrado do zinco custa M reais , calcule o preço total da peça

Passo 1

Oiii, nesse exercício podemos encontrar a área da superfície fazendo

∫ t 0 t 1 f σ t ⋅ σ ' t d t

Onde nossa função f será

f x , y , z = z

Como temos uma equação para z podemos substituir agora

x + y + z = 2

f x , y , z = 2 - x - y

Então só precisamos encontrar uma parametrização para nossa função

x 2 + y 2 = 4

σ t = 2 cos ⁡ t ,   2 sen ⁡ t

Vamos calcular σ ' t

σ ' t = - 2 sen ⁡ t ,   2 cos ⁡ t

σ ' t = 4 sen 2 ⁡ t + 4 cos 2 ⁡ t

σ ' t =   2

Estamos quase la, precisamos agora apenas descobrir nosso intervalo de integração. Nossa região podemos ver abaixo

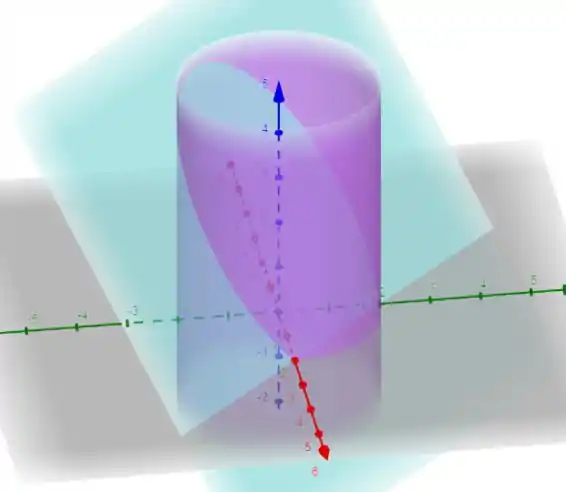
É a parte do plano interior ao cilindro. Podemos perceber que ele começa e termina no plano z = 0 . Então vamos olhar mais atentamente para ele

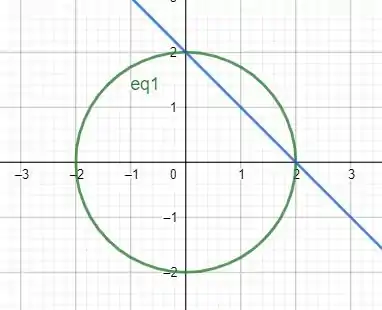
Olhando para as duas figuras podemos dizer que nossa superfície começa em 0,2 , 0 e termina em 2,0 , 0 . Podemos então dizer que em termos de t nosso intervalo é

t ∈ π 2 ,   2 π

Beleza temos agora tudo o que precisamos!!! Vamos integrar

Passo 2

∫ t 0 t 1 f σ t ⋅ σ ' t d t

∫ π 2 2 π ( 2 - 2 cos ⁡ t - 2 sen ⁡ t ) ⋅ 2 d t

2 ∫ π 2 2 π ( 2 - 2 cos ⁡ t - 2 sen ⁡ t ) d t

2 2 t - 2 sen ⁡ t + 2 cos ⁡ t t =   π 2 2 π

= 2 2   2 π - π 2 - 2 0 - 1 + 2 1 - 0

= 2 4 π - π

= 6 π

Como o custo por metro quadrado é M então nossa resposta

Custo = M ( 6 π )

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

Custo = M ( 6 π )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a massa do fio γ t = cos ⁡ ts e nt ,t , 0 ≤ t ≤ π , com densidade linear δ x , y , z = x 2 + y 2 + z 2
Calcule a massa do fio γ t = t , 2 t , 3 t , 0 ≤ t ≤ 1 , cuja densidade linear é δ x , y , z = x + y + z .
Calcule ∮ c fd S 1.f f x , y , z = x + y E C é a curva obtida como interseção do semiplano x = y y ≥ 0 Com o paraboloide z = x 2 + y 2 z ≤ 2
2. Um arame tem a forma da curva obtida como interseção da porção da esfera x 2 + y 2 + z 2 = 4 y ≥ 0 Com o plano x + z = 2 Sabendo-se que a densidade em cada ponto do arame é dada por f x , y , z = x