Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.7 - Ex. 71
Calcule a área da região que se encontra entre as curvas e de a
Passo 1
Lembre-se que para calcular a área entre curvas, precisamos saber qual curva que está por cima. Vamos usar um gráfico para tentar visualizar, beleza?
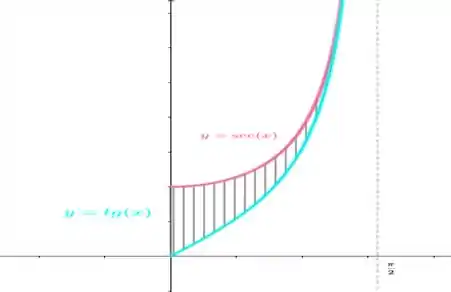
Então nossa área vai ser dada por:
Passo 2
Se olharmos para o gráfico direitinho ou só pensarmos um pouquinho a mais, da pra notar que quando , as funções do integrando não estão bem definidas, então, vamos dá uma mudada na integral. Ou seja,
Passo 3
Agora é só resolver nosso babado, usando as primitivas,
Passo 4
Fazendo a aplicação dos limites de integração,
Resposta
Exercícios de Livros Relacionados
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 1 ∞ x + 1 x 2 + 2 xd x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ - ∞ 1 x e 2 xd x
Mostre que se 0 ≤ f t ≤ M e a t para t ≥ 0 , onde M e a são constantes, então a transformada de Laplace F ( s ) existe para sa .
Determine o quão grande tem de ser o número a de modo que ∫ a ∞ 1 x 2 + 1d x0,001
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.