Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 9
Esboce a curva e calcule a área delimitada por ela.
Passo 1
Eaee, belezinha?? Bom... o enunciado é bem direto aqui!! A gente quer esboçar a seguinte curva e calcular a área dela:
Lembra de como encontramos a área de uma curva polar?? Assim, olha:
A gente vai determinar os limites de integração ao analisar seu gráfico, certinho?? Agora bora lá!! 😉
Passo 2
Vamos plotar o nosso gráfico... mas vamos começar assim: primeiramente vamos plotar no plano cartesiano para entendermos melhor, certinho??
A nossa curva é muito parecida com a curva do seno.
Mas, analisando a diferença entre as duas, temos que a nossa tem um multiplicando o seno. Isso significa que a amplitude do nosso seno dobra.
Assim, temos:
Passando para o plano polar, podemos ver que de a radianos, passa de para , logo:
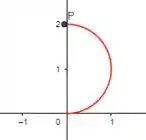
Em seguida, de a radianos, passa de para , fechando o ciclo:
Lembrando que como estamos utilizando coordenadas polares os valores de são positivos.
Passo 3
Agora vamos calcular nossa área!!
Quando calculamos a integral de uma curva, o resultado da integral fornece extamente a área da curva.
Vamos então integrar a fórmula para a área de uma região cuja fronteira é dada por uma equação polar.
Os limites de integração podemos encontrar a partir do gráfico.
A linha que forma a fronteira do gráfico começa em 0 e dá meia volta, ou seja, percorre um ângulo .
Nesse caso o ângulo não é , pois a cincunferência está deslocada para cima do eixo horizontal, desta forma o ângulo varre apenas dois quadrantes o que equivale a .
Passo 4
Aplicando os limites de integração e substituindo , obtemos:
Podemos usar a propriedade trigonométrica:
Resolvendo a integral:
Aplicando os limites de integração: