Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 54
Calcule o comprimento total da astroide com .
Passo 1
Fala ai pessoal! Tranquilo?
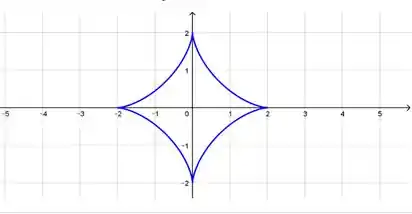
Vamos começar a calcular o comprimento total da astroide Mas você deve estar se perguntando: o que é um astroide? Não que isso interfira muito na resolução da questão, mas é legal conhecermos as figuras, astroide é o gráfico de um curva que se assemelha uma estrela, este é o gráfico do nosso astróide:
Passo 2
O comprimento de uma curva é
Vamos calcular primeiro a derivada das funções e em rela��ão a . Utilizando a regra da cadeira
Para :
Portanto,
Para
Portanto
Substituindo as derivadas na equação
Passo 3
Agora vamos jogar isso na nossa integral:
Então o comprimento do astroide é igual a .
Resposta
Então o comprimento do astroide é igual a .
Exercícios de Livros Relacionados
Reparametrizar pelo comprimento de arco as seguintes curvas: x = 1 - t ,y = 2 + 2 t ,z = 3 t ,t ∈ 0 , 1
Escrever a função comprimento de arco de:vec r (t) = (a cos^3 t , a s e n^3 t) , t in [0 , (pi)/(2)]
Reparametrizar pelo comprimento de arco as seguintes curvas: r → t = 2 cos t ,2 s e n t ,t ∈ 0 , 2 π
Reparametrizar pelo comprimento de arco as seguintes curvas: r → t = a cos 3 t ,as e n 3 t ,t ∈ 0 , π 2
Reparametrizar pelo comprimento de arco as seguintes curvas: r → t = cos 2 t ,s e n 2 t ,t ∈ 0 , π 2