Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.4 - Ex. 34

Calcule a integral

int (x^5 + x - 1)/(x^3 + 1) d x

Passo 1

Nossa integral é a seguinte: I = int (x^5 + x - 1)/(x^3 + 1) d x

Dividindo os polinômios, temos:

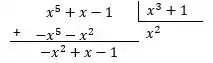
Isto é,

x^5 + x - 1 = (x^3 + 1) (x^2) + (- x^2 + x - 1)

Passo 2

Então nossa integral fica o seguinte:

I = int ((x^3 + 1) (x^2) + (- x^2 + x - 1))/(x^3 + 1) d x

Assim,

I = int (x^2 - (x^2 - x + 1)/(x^3 + 1)) d x

Separando em dois termos:

I = int x^2 d x - int (x^2 - x + 1)/(x^3 + 1) d x

Vou te lembrar uma fatoração que vai salvar nossa vida:

x^3 + 1 = (x + 1) (x^2 - x + 1)

Jogando isso na nossa integral:

I = int x^2 d x - int (x^2 - x + 1)/((x + 1) (x^2 - x + 1)) d x

Simplificando, temos:

I = int x^2 d x - int (1)/(x + 1) d x

Passo 3

Não esquece: int (1)/(x) d x = ln |x| + c

Agora vamos integrar!

I = int x^2 d x - int (1)/(x + 1) d x

Logo,

I = (x^(2 + 1))/(( 2 + 1 )) - ln |x + 1| + C

Portanto,

I = (x^3)/(3) - ln |x + 1| + C

Resposta

I = (x^3)/(3) - ln |x + 1| + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

v = (( t + 3 ))/(( t + 1 ) ( t + 2 ))
(d x)/(d t) = k (5 - x) (4 - x) int (d x)/((5 - x) (4 - x)) = int k d t