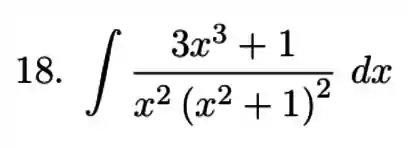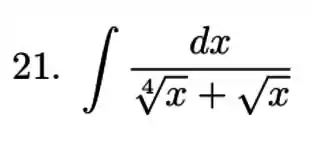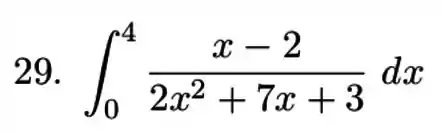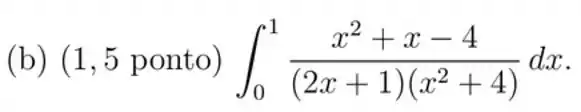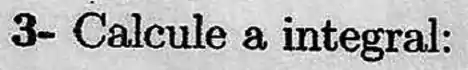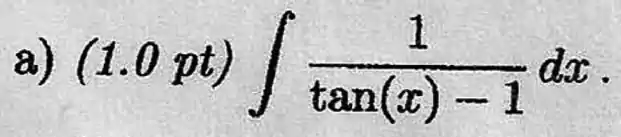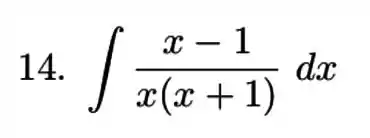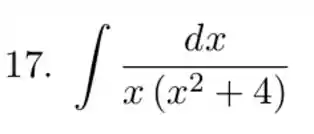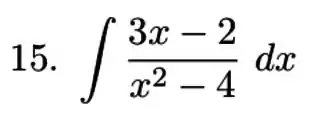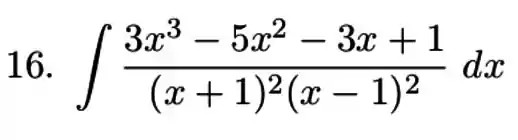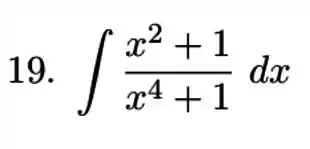Exercícios de Integrais com Frações Parciais - Lista de Exercícios Resolvida
Questão 26
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
5)
Ver solução completaQuestão 27
Qual das seguintes afirmações é verdadeira:
Escolha uma opção:
, onde , e são constantes a serem determinadas
, para
, onde
Ver solução completa
Questão 30
Um aluno escreveu na prova
1. Sem calcular a integral, mostre que a resposta está errada.
2. Calcule a integral corretamente.
Ver solução completaQuestão 41
Obtenha uma primitiva (integral indefinida) para a função racional
que satisfaz a condição .
Sugestão: Escreva na forma
Ver solução completaQuestão 62
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
10)
Ver solução completaQuestão 68
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
9)
Ver solução completaQuestão 69
A velocidade de uma partícula se movendo ao longo de uma linha é uma função do tempo dada por
Encontre a distância que a partícula viajou após
Ver solução completaQuestão 70
Use substituição para converter a integral abaixo em integral de funções racionais, e em seguida resolva a integral
Ver solução completaQuestão 71
Use substituição para converter a integral abaixo em integral de funções racionais, e em seguida resolva a integral
Ver solução completaQuestão 80
Use a decomposição de fração parcial (ou uma técnica mais simples) para expressar a função racional abaixo como uma soma ou diferença de duas ou mais expressões racionais mais simples.
Ver solução completaQuestão 83
Use a decomposição de fração parcial (ou uma técnica mais simples) para expressar a função racional abaixo como uma soma ou diferença de duas ou mais expressões racionais mais simples.
Ver solução completaQuestão 87
Use a decomposição de fração parcial (ou uma técnica mais simples) para expressar a função racional abaixo como uma soma ou diferença de duas ou mais expressões racionais mais simples.
Ver solução completaQuestão 99
Use substituição para converter a integral abaixo em integral de funções racionais, e em seguida resolva a integral
Ver solução completaQuestão 103
Os únicos valores de e para os quais
onde é uma constante arbitrária, são
a) e
b) e
c) e
d) e
e) e
Ver solução completaQuestão 109
Resolva, desenvolvendo detalhadamente, as integrais abaixo. (Obs.: Não é permitido propor primitivas e derivá-las. As integrais devem ser resolvidas!)
Questão 110
Resolva, desenvolvendo detalhadamente, as integrais abaixo. (Obs.: Não é permitido propor primitivas e derivá-las. As integrais devem ser resolvidas!)
Questão 115
3) Para cada uma das funções abaixo, determine o formato da sua expressão em frações parciais. Aqui, não é necessário calcular as constantes mas somente apresentar o formato da soma.
a)
Ver solução completaQuestão 117
3) Para cada uma das funções abaixo, determine o formato da sua expressão em frações parciais. Aqui, não é necessário calcular as constantes mas somente apresentar o formato da soma.
d)
Ver solução completaQuestão 119
3) Para cada uma das funções abaixo, determine o formato da sua expressão em frações parciais. Aqui, não é necessário calcular as constantes mas somente apresentar o formato da soma.
f)
Ver solução completaQuestão 140
Use substituição para converter a integral abaixo em integral de funções racionais, e em seguida resolva a integral
Ver solução completaQuestão 141
Use substituição para converter a integral abaixo em integral de funções racionais, e em seguida resolva a integral
Ver solução completaQuestão 142
3) Para cada uma das funções abaixo, determine o formato da sua expressão em frações parciais. Aqui, não é necessário calcular as constantes mas somente apresentar o formato da soma.
e)
Ver solução completaQuestão 149
2. Resolva as seguintes integrais usando o método das frações parciais:
d)
Ver solução completaQuestão 150
2. Resolva as seguintes integrais usando o método das frações parciais:
g)
Ver solução completaQuestão 151
2. Resolva as seguintes integrais usando o método das frações parciais:
f)
Ver solução completaQuestão 169
Determinar a integral
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido os valores para os fatores ; ; e e a resposta final não foi possível determinar.
Ver solução completaQuestão 180
Determinar a integral
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido valores para os fatores ; ; e e a resposta final foi correspondente a .
Na resolução desta integral foi obtido os valores para os fatores ; ; e e a resposta final não foi possível determinar.
Ver solução completaQuestão 190
Calcule as seguintes integrais, usando o método das frações parciais:
Ver solução completaQuestão 191
Calcule as seguintes integrais, usando o método das frações parciais:
Ver solução completaQuestão 192
Calcule as seguintes integrais, usando o método das frações parciais:
Ver solução completaQuestão 193
Calcule as seguintes integrais, usando o método das frações parciais:
Ver solução completaQuestão 194
Seja um integrando dado por uma fração em que o numerador e o denominador são expressões algébricas envolvendo e/ou . Nete caso, a mudança de variável pode ser um método recomendado. Temos as igualdades:
Consequentemente, a integral original é transformada em uma integral em que o integrando é uma função racional e, quase sempre o método das frações parciais pode ser aplicado.
Aplique esse método para encontrar uma primitiva para seguintes integrais
Ver solução completaQuestão 195
Seja um integrando dado por uma fração em que o numerador e o denominador são expressões algébricas envolvendo e/ou . Nete caso, a mudança de variável pode ser um método recomendado. Temos as igualdades:
Consequentemente, a integral original é transformada em uma integral em que o integrando é uma função racional e, quase sempre o método das frações parciais pode ser aplicado.
Aplique esse método para encontrar uma primitiva para seguintes integrais
Ver solução completaQuestão 196
9.8 Seja
a) Para e , escreva a expansão de em frações parciais (não precisa calcular os coeficientes).
Ver solução completaQuestão 199
10.6
b) A integral
Resulta numa expressão da forma
Onde é a constante de integração. Determine os valores de .
Ver solução completaQuestão 200
10.6
a) Escreva a decomposição em frações parciais de
Você não precisa calcular os valores das constantes, somente exibir como será a composição.
Ver solução completaQuestão 201
Substituições trigonométricas e frações parciais
Calcule (inicialmente escolha os valores de )
Ver solução completaQuestão 202
Frações parciais mais complicadas, comprimento de arco e volume
Encontre a decomposição em frações parciais da integral
Ver solução completaQuestão 203
A integral é equivalente a uma certa integral de uma fração racional. Qual é esta integral?
Ver solução completaQuestão 204
A integral é equivalente a uma cerca integral de uma função racional. Qual é esta integral?
Ver solução completaQuestão 206
Resolva até onde conseguir a integral (Pelo menos transforme-a numa integral de uma função racional e use a decomposição em frações parciais.)
Ver solução completaQuestão 207
Calcule as seguintes integrais, usando o método das frações parciais:
Ver solução completaQuestão 208
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 209
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 210
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 211
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 212
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 213
Resolva as seguintes integrais usando o método das frações parciais:
Ver solução completaQuestão 217
6. Frações parciais
e) Obtenha uma primitiva para a função racional , onde , e satisfaz .
Ver solução completa