Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.1 - Ex. 48
Calcule a integral Algumas integrais não requerem integração por partes.
Passo 1
O enunciado pede que para resolvermos essa integral e afirma que nem todas as integrais são calculadas por meio de integração por partes. Nessa questão usaremos integração tabular, que é um caso de repetição da integração por partes.
Apesar de se tratar de uma integral definida iremos, inicialmente, resolver como se fosse indefinida para facilitar o cálculo e depois aplicar a integral definida.
Passo 2
Separamos em f(x) = e g(x) =, e seguida montamos a tabela:
f(X) e suas derivadas g(x) e suas integrais
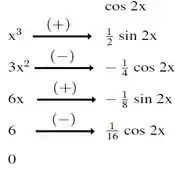
Para integrar g(x) usamos a fórmula: , e
sendo “k” uma constante.
Depois multiplicamos as funções ligadas e combinamos elas de acordo com os sinais das operações indicadas.
Passo 3
Aplicar a integral definida no resultado