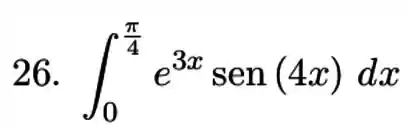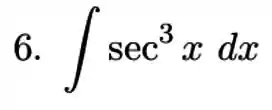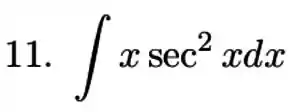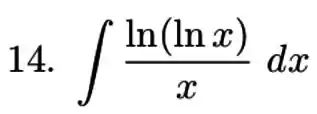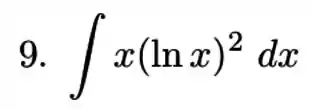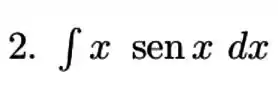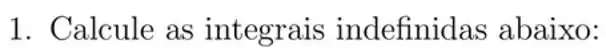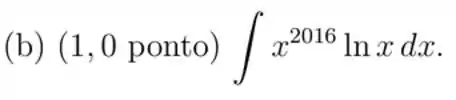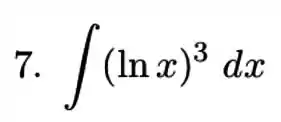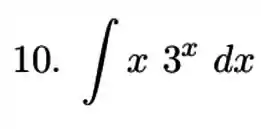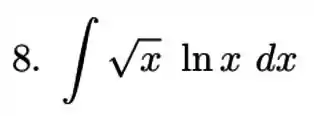Exercícios de Integração por Partes - Lista de Exercícios Resolvida
Questão 6
Calcule a integral indicada, utilizando a técnica de integração por partes.
Ver solução completaQuestão 35
2) Calcule
- Considere a EDO “”. Determine a solução geral da EDO e encontre a solução da mesmaque satisfaz a condição inicial .
Questão 38
1.4. Calcule as integrais abaixo (usando linearidade ou diretamente):
(a)
Ver solução completaQuestão 39
1.4. Calcule as integrais abaixo (usando linearidade ou diretamente):
(b)
Ver solução completaQuestão 44
3.3. Calcule usando integração por partes. Mostre o que acontece se você não fizer uma boa escolha inicial de e .
Ver solução completaQuestão 52
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
1)
Ver solução completaQuestão 53
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
12)
Ver solução completaQuestão 54
Nos exercícios a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
14)
Ver solução completaQuestão 55
Nos exercício a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
17)
Ver solução completaQuestão 67
Para a integral abaixo, determine seu valor ou decida sobre sua convergência.
Ver solução completaQuestão 87
Um corpo se move em uma reta com velocidade . No instante inicial ele estava na posição . Sua localização no instante é igual a:
Questão 102
Calcule a integral indicada, utilizando a técnica de integração por partes.
Ver solução completaQuestão 104
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
1)
Ver solução completaQuestão 105
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
4)
Ver solução completaQuestão 114
Explique que procedimento usar para calcular a integral (não precisa calcular, apenas o caminho)
Ver solução completaQuestão 136
Seja função duas vezes diferenciável tal que e
O valor da integral é:
Questão 140
Seja uma função contínua que não se anula para tal que é satisfeito:
- Calcule para esse intervalo, se for necessário usar uma integral, aplique primeiro uma substituição e depois uma integral por frações parciais, outros métodos serão desconsiderados.
- Calcule .
Questão 145
Determinar o valor da integral
Obs.: para solução deve ser usado inicialmente o método de integração por partes e, pelo menos uma vez, o método da substituição.
Ver solução completaQuestão 149
6) Após identificar a técnica apropriada, determine o valor das integrais abaixo.
g)
Ver solução completaQuestão 151
Use o método de integração por partes para calcular as integrais abaixo.
Ver solução completaQuestão 170
Calcule as integrais abaixo usando, antes da integração por partes, uma substituição apropriada.
Ver solução completaQuestão 171
Calcule as integrais abaixo usando, antes da integração por partes, uma substituição apropriada.
Ver solução completaQuestão 172
Após identificar a técnica apropriada, determine o valor das integrais abaixo
Ver solução completaQuestão 174
6) Após identificar a técnica apropriada, determine o valor das integrais abaixo.
d)
Ver solução completaQuestão 181
Responda os itens com respeito à integral
a) Utilize a fórmula de integração por partes fazendo e e determine o valor da integral.
b) Utilize a fórmula de integração por partes fazendo e e comente por que essa escolha não é boa.
c) A integral representa o volume de um sólido gerado pela de revolução de uma região, em torno do eixo . Descreva as curvas que delimitam essa região no plano.
Ver solução completaQuestão 194
Calcule as integrais abaixo usando, antes da integração por partes, uma substituição apropriada.
Ver solução completaQuestão 209
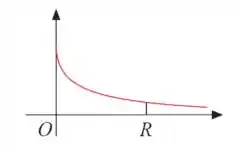
A figura ao lado ilustra o gráfico da função , . A área sob esse gráfico entre e é dada pela integral
Use uma mudança de variáveis para transformar a integral indefinida em uma outra cujo integrando não envolva a função raiz quadrada.
Calcule a integral do item anterior usando integração por partes.
Usando os resultados anteriores, determine explicitamente a função .
Calcule o limite usando a regra de L’Hospital, e verifique se a área sob o gráfico da , para , é finita.
Questão 211
Uma partícula se move sobre o gráfico da equação , com , e tem velocidade horizontal , . Sabendo que para , a partícula passa pelo ponto , encontre a posição da partícula, e o vetor velocidade no tempo .
Ver solução completaQuestão 233
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 234
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 235
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 236
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 237
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 238
Determine as seguintes integrais usando o método de integração por partes
Ver solução completaQuestão 239
Calcule utilizando ora integração por substituição, ora integração por partes
Ver solução completaQuestão 240
Usando recursivamente a integração por parte obtenha as seguintes fórmulas de recorrências
Ver solução completaQuestão 244
Usando integração por parte determine as seguintes fórmulas de recorrência
Ver solução completaQuestão 246
Usando integração por parte determine as seguintes fórmulas de recorrência
Ver solução completaQuestão 254
Calcule as integrais abaixo usando o método de integração por partes
Ver solução completaQuestão 255
Determine as seguintes integrais usando o método de integração por partes
Ver solução completaQuestão 256
Determine as seguintes integrais usando o método de integração por partes
Ver solução completaQuestão 257
Calcule a seguinte integral usando primeiramente o método de substituição e depois, integração por partes:
Ver solução completaQuestão 258
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 259
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 260
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 261
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 262
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 263
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 264
Resolva as seguintes integrais pelo método da integração por partes:
Ver solução completaQuestão 272
Use o método de integração por partes para calcular as integrais abaixo.
Ver solução completaQuestão 273
Use o método de integração por partes para calcular as integrais abaixo.
Ver solução completaQuestão 274
Use o método de integração por partes para calcular as integrais abaixo.
Ver solução completaQuestão 275
Use o método de integração por partes para calcular as integrais abaixo.
Ver solução completa