Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 38
Calcule a integral, interpretando-a em termo de áreas.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente calcular a integral abaixo, interpretando-a em termos das áreas.
Sendo assim, vamos olhar pra a função que está sendo integrada e desenhar seu gráfico. Isso vai nos ajudar a entender essa integral como sendo um cálculo de área.
Vem comigo.
Passo 2
O que a questão nos pede é para calcularmos a integral, porém resolvendo ela utilizando o conceito de que uma integral é a área abaixo do gráfico da função, delimitada pelos limites de integração da integral dada.
Vamos desenhar o gráfico, da função para analisarmos qual a área dada.
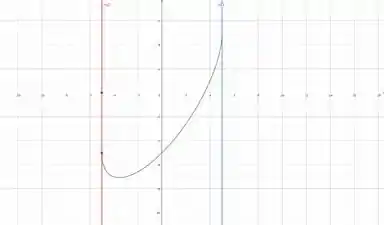
Perceba que a área da região que precisamos calcular não é tão trivial. Mas, e se utilizarmos a propriedade
Agora temos duas regiões, vamos dar uma olhadinha nelas:
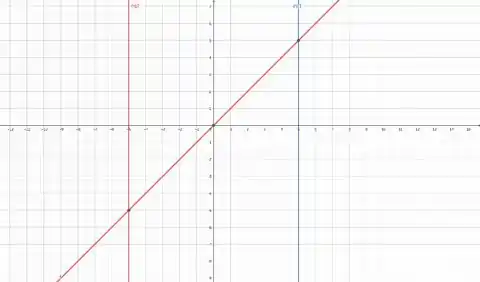
Para a primeira integral temos a área resultante desses 2 triângulos,
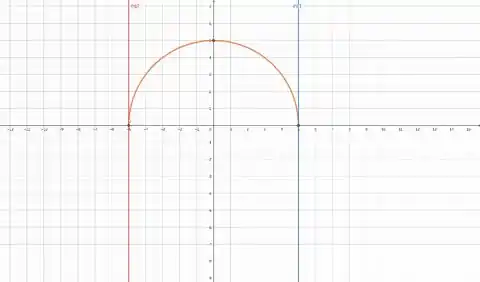
E para a segunda integral temos um semicírculo.
Passo 3
Calculando a área dos 2 triângulos:
Temos então que
Como temos que subtrair de , a área resultante é 0.
Passo 4
Agora vamos calcular a área da semicircunferência:
Podemos observar pelo gráfico que temos um raio de 5.
Passo 5
Substituindo, calculando a área total: