Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 35
35 - 40. Calcule a integral, interpretando-a em termos das áreas.
35)
Passo 1
E aí, pessoal!
Nesse problema temos que calcular a integral pelo gráfico, bora lá
Veja só!
Passo 2
Temos a função que é , vamos traçar ela no plano cartesiano. Para os limites da integração, traçaremos duas retas, e .
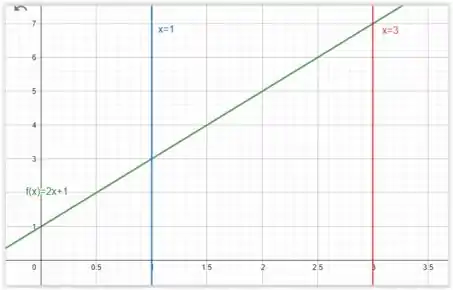
Tranquilo até aqui?
Passo 3
O problema nos pediu para interpretar esse resultado como uma área! Vamos fechar nossa função com o .
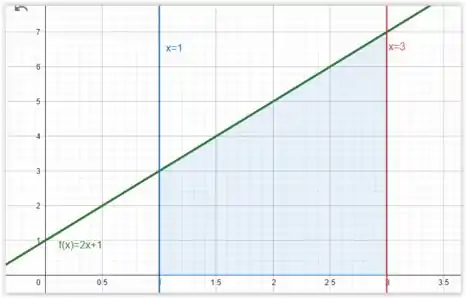
Dividindo nosso gráfico em 2 partes:
1ª um retângulo de base e altura
2ª Um triangulo com base e altura
Calculando as áreas, temos:
Retângulo
Triângulo
Somando as áreas
E aí! entendeu tudo? Responde Aí!
Resposta
Valor correspondente a área do gráfico de até ao eixo para de a .
Exercícios de Livros Relacionados
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Determine a norma da partição P = { 0 ; 1.2 ; 1.5 ; 2.3 ; 2.6 ; 3 }
Determine a norma da partição P = { - 2 ; - 1 . 6 ; - 0 . 5 ; 0 ; 0.8 ; 1 }
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ