Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 3b
Calcule a integral de linha por dois métodos:
(b) utilizando o Teorema de Green.
é um triângulo com os vértices em e .
Passo 1
Faala, pessoal!
Nessa questão vamos usar o Teorema de Green pra calcular uma integral de linha:
O teorema diz o seguinte:
Onde é uma curva fechada e é a região dentro dessa curva.
Pra resolver essa questão, vamos começar esboçando a curva , e a região , pra conferirmos se é realmente uma curva fechada e podemos aplicar o teorema.
Depois, vamos definir os limites de integração de , calcular , e colocar tudo na equação do teorema. Daí, nosso trabalho vira calcular uma integral dupla.
Vamos lá?
Passo 2
Primeiro, nossa curva é um triângulo com os vértices em e .
Desenhando, fica assim:
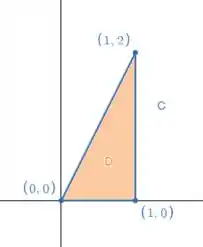
Então, nossa curva é de fato uma curva fechada e podemos aplica o teorema!
Passo 3
Agora vamos focar na região . Precisamos dos limites de integração dela.
Essa região é limitada por:
E com relação a , está entre a reta que liga a e o eixo . Vamos achar a equação dessa reta. Como ela passa pelo , seu coeficiente linear é . O coeficiente angular é:
Então:
E a região é limitada por:
Percebe que como os limites de dependem de , vamos integrar primeiro em função de . Ou seja, nossa integral vai ficar assim:
Passo 4
Falta acharmos esse termo .
Como a integral que estamos calculando é
Temos que:
Então, vamos calcular as derivadas parciais.
Primeiro de em função de , considerando constante:
E agora derivamos em função de com constante:
Então a integral fica assim:
Passo 5
Finalmente, só falta calcular essa integral dupla.
Calculamos de dentro pra fora, primeiro em função de , com constante:
Simplificando e substituindo os limites de integração
E por último, vamos integrar em função de :
Aplicando os limites: