Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 2a
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.
é uma circunferência com centro na origem e .
Passo 1
Que tal desenharmos a curva primeiro de tudo?!
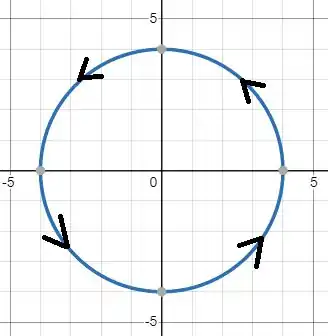
Pra começar, podemos parametrizar a curva para facilitar a nossa integração! A representação paramétrica de uma circunferência é dada por:
Portanto,
Os limites de integração serão de a , pois por convenção, o caminho deve ser orientado em sentido anti-horário.
Passo 2
Nossa integral é dada por
Substituindo os limites de integração e os valores de , temos:
Resposta
A integral de linha é igual a:
Exercícios de Livros Relacionados
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.
Use o Use o teorema de Green para calcular ∫ C F → ⋅ d r → . (Verifique a orientação da curva antes de aplicar o teorema.)
Use o Use o teorema de Green para calcular ∫ C F → ⋅ d r → . (Verifique a orientação da curva antes de aplicar o teorema.)
Use o Use o teorema de Green para calcular ∫ C F → ⋅ d r → . (Verifique a orientação da curva antes de aplicar o teorema.)