Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 18
Esboce o sólido cujo volume é dado pela integral e calcule o valor da integral.
Passo 1
E aí, meus amigos! Tudo joia?
Nossa questão pede pra gente esboçar o volume que a integral:
Está descrevendo. Temos que essa integral acima é a integral de volume de um sólido que está escrito em coordenadas esféricas, onde:
Das equações de transformação para coordenadas esféricas, temos:
Então, as informações sobre o sólido que a integral dá estão nos limites de integração de cada variável.
Então, através dos limites de integração em coordenadas esféricas e suas relações com as coordenadas cilíndricas, conseguimos entender qual sólido está tendo seu volume descrito.
Depois é só resolvermos nossa integral tripla de forma iterada, começando de dentro para fora!
Vambora!
Passo 2
Analisando o intervalo de integração em , temos:
Analisando um dos extremos desse intervalo:
Isolando o , ficamos com:
Podemos substituir o valor da equação de transformação para . Como:
ficamos com:
Então, para coordenadas retangulares, temos que:
Para as demais variáveis, vemos que:
Ou seja, teremos uma linha que parte da parte positiva de até e como temos todos os valores de possíveis, essa linha vai percorrer todo o entorno do eixo .
Nesse caso, a região dada é acima do cone com e abaixo do plano . A superfície está ilustrada na figura a seguir:
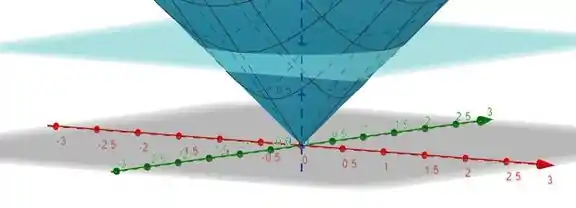
Passo 3
Agora iremos resolver a integral:
Resolvendo para que é nossa integral de dentro, e tratando as demais variáveis como constante, temos:
Aplicando os limites de integração:
Passo 4
Agora, separando em e :
E, resolvendo cada integral com sua respectiva variável de integração, obtemos:
Sendo assim, temos que: