Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.2 - Ex. 8
Calcule a integral de linha, onde é a curva dada.
consiste na metade superior da circunferência de a e o segmento de reta de a e o segmento de reta de a .
Passo 1
O problema pede para calcularmos a integral de linha sobre a curva dada:
Aqui a curva é composta de duas partes:
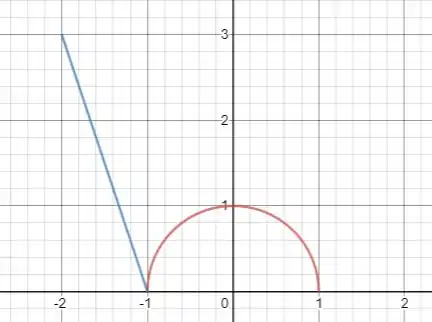
Vamos fazer primeiro a integral sobre o círculo:
Assim,
Portanto,
Na primeira integral fazemos a substituição . Já na segunda, fazemos :
Portanto,
Mas como :
Passo 2
Já para reta, usamos
Assim,
Logo,
A primeira integral é simples:
Como
A segunda integral pode ser reescrita como
Fazemos agora :
Portanto,
Logo,
Assim,
Resposta
Exercícios de Livros Relacionados
Determine o trabalho realizado pelo campo de força F → ao mover um objeto de P a Q . F → x , y = 2 y 3 / 2 i → + 3 x y j → ;P 1,1 ,Q ( 2,4 )
Determine o trabalho realizado pelo campo de força F → ao mover um objeto de P a Q . F → x , y = e - y i → - x e - y j → ;P 1,1 ,Q ( 2,0 )
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 1 + x 2 i → + 2 y a r c t g xj → ,C : r → t = t 2 ,2 t , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = x y 2 i → + x 2 y j → ,C : r → t = t + s e n 1 2 π t ,t + cos 1 2 π t , 0 ≤
A figura abaixo mostra o campo vetorial F → x , y = 2 x y , x 2 e três curvas que começam em ( 1,2 ) e terminam em ( 3,2 ) . Explique por que ∫ C F → ⋅ d r → tem o mesmo valor para as três curvas.Qual