Exercícios de Caso Vetorial no R² - Lista de Exercícios Resolvida

Calcule

Onde é a curva:

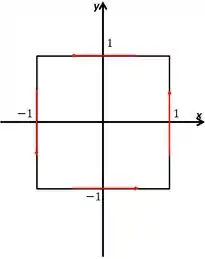
Calcule a integral de linha , onde é o triângulo com vértices nos pontos , e .

Considere a integral de linha

Onde é a fronteira da região do primeiro quadrante limitada pelas circunferências e , orientada no sentido anti-horário e é o campo vetorial definido por

Calcule Essa integral pela definição de integral de linha.

Calcule o trabalho realizado pela força ao mover uma partícula da origem ao longo do eixo até , em seguida ao longo do seguimento de reta até , e então de volta à origem ao longo da curva

Seja uma função contínua sobre um arco regular de comprimento L. Se , em todos os pontos do arco , mostre que:

Calcule , nos seguintes casos:

(a) ; é o círculo .

Calcule onde é o segmento de reta contido no interior da elipse e orientado no sentido de crescente.

Sob ação da força , um objeto percorre a elipse , no sentido anti-horário. Qual o trabalho realizado pelo campo ?

1. Calcule de a ao longo

1. de :

1. Achar o trabalho de uma força variável, dirigida para a origem das coordenadas, cuja grandeza é proporcional ao afastamento do ponto em relação à origem das coordenas, se o ponto de aplicação desta força descreve, no sentido anti-horário, a parte da elipse no primeiro quadrante.

Uma partícula de peso desce de a ao longo da parábola . Agem sobre a partícula a força de gravidade e também uma força horizontal dirigida para a direita, de módulo igual à coordenada do ponto. Determine o trabalho realizado por essas duas forças.

Calcule a integral de linha , onde  , ao longo de cada curva plana dada abaixo, do ponto ao ponto

(a) é a parábola

Seja

um campo vetorial em . Calcule a integral de linha do campo ao longo da curva , orientada no sentido anti-horário, onde:

é a circunferência de equação .

Considere a curva

Definida para , e a função escalar

Definida sobre o traço de .

1. Esboce o traço de e calcule
2. Exprima o comprimento de como uma integral definida (não precisa resolver a integral, mas simplifique)
3. Se o traço de for interpretado como um fio e for interpretado como a densidade linear de carga elétrica no ponto desse fio, qual é a interpretação correspondente para
4. Existe um campo vetorial tal que ?

1. Calcule de a ao longo

1. do eixo

(5) A integral do campo vetorial ao longo da curva , , é igual a

1. Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.

1. circunferência de centro na origem e raio .

1. Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.

1. Elipse .

1. Calcule de a , ao longo

1. do segmento de reta.

1. Calcule de a , ao longo

1. do arco da parábola .

Calcule o trabalho realizado pela força ao mover uma partícula da origem ao longo da reta até e então de volta à origem ao longo da curva

Calcule a integral de linha , onde  , ao longo de cada curva plana dada abaixo, do ponto ao ponto

(b) é a curva dada por

Considere a linha poligonal fechada C de vértices , , percorridos no sentido anti-horário. Para o campo vetorial

Calcule

. Calcule

onde é a porção do círculo no primeiro quadrante percorrida no sentido do ponto para o ponto .

. Calcule

onde é a porção do círculo no primeiro quadrante percorrida no sentido do ponto para o ponto .

Decida se as afirmações abaixo são verdadeiras ou falsas, justificando. (aviso: resposta errada ou resposta certa sem justificativa receberá zero no item respectivo).

Se é o círculo unitário com centro na origem, então:

(Cap.16.2 - Ex.39) Determine o trabalho realizado pelo campo de força sobre um objeto que se move sobre um arco da cicloide .

(Cap.16.3 - Exercício 3) Determine se é ou não um campo vetorial conservador. Se for, determine uma função tal que

(Capítulo 16.2 – Exercício 40) Determine o trabalho realizado pelo campo de força em uma partícula que se move sobre a parábola de a .

(Cap.16.3 - Exercício 5) Determine se é ou não um campo vetorial conservador. Se for, determine uma função tal que .

(Cap.16.3 - Exercício 7) Determine se é ou não um campo vetorial conservativo. Se for, determine uma função tal que

(Cap.16.3 - Exercício 12) (a) Determine uma função tal que e (b) Use a parte (a) para calcular sobre a curva dada.

é o arco da parábola de a

Considere os vértices , , conforme figura abaixo.

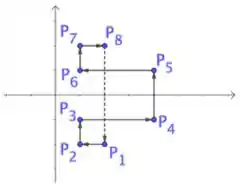
FIGURE . Linhas poligonais com vértices . No item , o lado tracejado não está incluído na linha poligonal. No item , todos os lados estão na linha poligonal.

Considere também o campo vetorial

Para a linha poligonal aberta de vértices percorridos no sentido indicado na figura, calcule

Para a linha poligonal fechada de vértices percorridos no sentido indicado na figura, calcule

Seja .

1. Calcule

onde é a curva

7. Calcule , sendo dados:

c) e , .

7. Calcule , sendo dados:

d) e , .

8. Uma partícula move-se no plano de modo que no instante sua posição é dada por . Ache o trabalho realizado pelo campo de forças no deslocamento da partícula de até .

10. Calcule onde e , .

(Cap.16.3 - Exercício 23) Determine o trabalho realizado pelo campo de força ao mover um objeto de para .

Questão 3: Calcule a integral de linha do campo vetorial ao longo da curva dada pela equação , do ponto até o ponto .

Considere a integral de linha

Onde é a fronteira da região do primeiro quadrante limitada pelas circunferências e e é o campo vetorial definido por

Calcule Essa integral pela definição de integral de linha.

Calcule a integral de linha , onde e é dada pela função vetorial

Calcule a integral de linha

Onde e é a elipse

Percorrida no sentido anti-horário.

Sejam   e a curva com . Então é:

2) Seja o campo dado por:

Calcule onde e é o vetor unitário apontando para fora de .