Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 14

Calcule a integral tripla

∭ E x + 2 y d V , onde E é limitado pelo cilindro parabólico y = x 2 e pelos planos x = z , x = y   e z = 0 .

Passo 1

E aí, fera dos cálculos! Está na hora de resolver mais um desafio. Vamos que vamos!

Para solucionar essa questão vamos resolver a integral tripla ∭ E x + 2 y d V , onde E é limitado pelo cilindro parabólico y = x 2 e pelos planos x = z , x = y   e z = 0 .

Temos a seguinte situação descrita no enunciado:

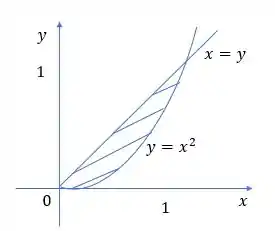
E é o sólido acima da região mostrada no plano x y e abaixo do plano z = x .

Passo 2

Então, podemos escrever nossa integral tripla:

∭ E x + 2 y d V = ∫ 0 1 ∫ x 2 x ∫ 0 x x + 2 y d z d y d x

Passo 3

Vamos calcular essa integral, de fora para dentro. Primeiramente, integramos em relação a z :

∫ 0 1 ∫ x 2 x ∫ 0 x x + 2 y d z d y d x

Integrando x + 2 y em relação a z de 0 a x :

∫ 0 1 ∫ x 2 x x + 2 y z z = 0 z = x d y d x

Isso resulta em:

∫ 0 1 ∫ x 2 x x + 2 y x   d y d x = ∫ 0 1 ∫ x 2 x x 2 + 2 y x   d y d x

Agora, integramos em relação a y :

∫ 0 1 x 2 y + x y 2 y = x 2 y = x d x =

Substituindo os limites de y :

∫ 0 1 x 2 ( x ) + x ( x 2 ) - x 2 ( x 2 ) + x ( x 4 ) d x = ∫ 0 1 x 3 + x 3 - ( x 4 + x 5 ) d x

Simplificando a expressão dentro da integral:

∫ 0 1 ( 2 x 3 - x 4 - x 5 ) d x

Agora, integramos em relação a x :

∫ 0 1 ( 2 x 3 - x 4 - x 5 ) d x = 2 4 x 4 - 1 5 x 5 - 1 6 x 6 0 1

Calculando as integrais:

1 2 x 4 - 1 5 x 5 - 1 6 x 6 0 1 = 1 2 ( 1 - 0 ) - 1 5 ( 1 - 0 ) - 1 6 ( 1 - 0 )

= 1 2 - 1 5 - 1 6 - 0

Encontrando o denominador comum, ficaremos com:

1 5 30 - 6 30 - 5 30 = 4 30

Simplificando:

= 2 15

Resposta

2 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por z = x 2 + y 2 , z = 2
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T y + x 2 z d V Onde T é paralelepípedo retângulo 1 ≤ x ≤ 2 ,0 ≤ y ≤ 1 ,- 3 ≤ z ≤ 5 .
Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + y 2 + z 2 = a 2
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T z d V Onde T é o solido limitado por z = 0,y = z , y = 2 - x 2 .
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T d x d y d z x + y + z + 1 2 Sendo T é o solido delimitado pelos planos coordenados e pelo plano x + y + z= 2 .