Calcule a inversa da matriz dada ou mostre que ela é singular:

Antes de calcular o determinante da matriz precisamos reduzir sua ordem. Para isso vamos aplicar a regra de Chió. Ela é dada por:

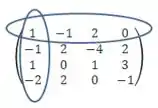
Encontramos um coeficiente igual a 1. Então selecionamos a linha e a coluna do coeficiente. Dos termos que restaram devemos subtrair a multiplicação dos termos correspondentes na linha e coluna que retiramos. Vamos fazer pegar um termo para exemplificar:

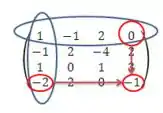
O termo na matriz original é -1. Na coluna em que ele estava retiramos o número 0 e, na linha em que ele estava retiramos o número -2. Tudo bem???

Na matriz reduzida este termo será . Fez sentido agora? Vamos então determinar a matriz reduzida:

Agora que temos uma matriz 3x3 podemos calcular o determinante:

Então, a matriz é inversível. Vamos agora determinar a matriz inversa.

O método mais comum é o seguinte:

Espelhar a matriz e a identidade. Em seguida vamos tentar transformar a matriz na matriz identidade:

Vamos começar somando a primeira linha na segunda:

Agora iremos subtrair a primeira da terceira linha:

Vamos agora multiplicar a primeira linha por 2 e somar na quarta:

Iremos agora subtrair a segunda linha da terceira:

Nosso próximo passo será multiplicar a terceira linha por 4 e subtrair da quarta linha:

Agora, vamos somar multiplicar a quarta linha por -1/5:

Iremos agora subtrair a quarta linha da terceira:

Nosso próximo passo será multiplicar a terceira linha por 2 e somar na segunda linha:

Vamos agora multiplicar a quarta linha por 2 e subtrair da segunda linha:

Agora, iremos somar a segunda linha na primeira:

Nosso último passo será multiplicar a terceira linha por 2 e subtrair da primeira linha:

Então, a matriz inversa é: