Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 11

Considere uma barra com 30 cm de comprimento para a qual α 2 = 1 . Suponha que a distribuição inicial de temperatura é dada por u(x, 0) = x(60 – x)/30 e que as condições de contorno são u(0, t) = 30 e u(30, t) = 0.

  1. Encontre a temperatura na barra em função da posição e do tempo.
  2. Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
  3. Faça o gráfico de u em função de t para x = 12. Note que u inicialmente diminui, depois cresce por um tempo e, finalmente, diminui para alcançar seu valor no estado estacionário. Explique, fisicamente, por que esse comportamento ocorre nesse ponto.

Passo 1

O problema é:

u x x = u t ,   0 < x < 30 ,   t > 0

u ( 0 , t ) = 30 ,   t > 0

u ( 30 , t ) = 0 ,   t > 0

u ( x , 0 ) = x ( 60 - x ) 30 ,   0 < x < 30

Temos L = 20 :

A solução é dada pelas fórmulas 16 e 17 na página 634:

u ( t , x ) = ( T 2 - T 1 ) x L + T 1 + ∑ n = 1 ∞ c n e - n ² π ² α ² t L ² s e n ( n π x L )

c n = 2 L ∫ 0 L [ f ( x ) - ( T 2 - T 1 ) x L - T 1 ]   s e n ( n π x L ) d x

Passo 2

Temos L = 30 ,   α ² = 1 ,   f ( x ) = x ( 60 - x ) 30 ,   u ( 0 , t ) = T 1 = 30 ,   u ( L , t ) = T 2 = 0

Queremos c n :

c n = 60 n ³ π ³ [ 2 ( 1 - c o s ( n π ) ) - n ² π ² ( 1 + c o s ( n π ) ) ]

Substituímos e achamos:

u ( t , x ) = 30 - x + ∑ n = 1 ∞ 60 n ³ π ³ [ 2 ( 1 - c o s ( n π ) ) - n ² π ² ( 1 + c o s ( n π ) ) ] e n ² π ² t 900 s e n ( n π x 30 )

Passo 3

Na letra b:

u versus t, para x=5,15, 20:

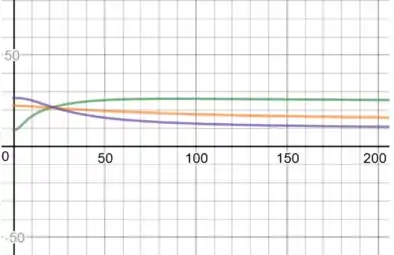
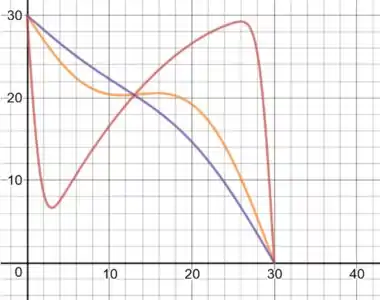
u versus x, para t=1,30,60:

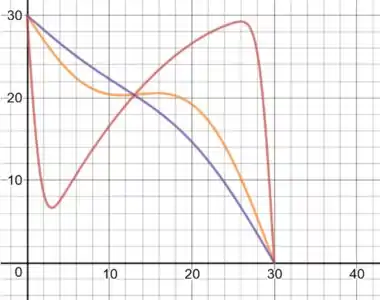
Passo 4

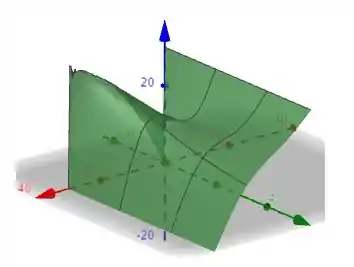
Na letra c:

u versus t para x=12. Podemos ver que u decresce, depois cresce um pouco, e finalmente decresce até chegar a um valor constante. Quando x=12, u começa a partir de u ( 12,0 ) = 12 ( 60 - 12 ) 30 = 19.2 e tende para 30 - 12 = 18 .

Fisicamente, u começa a tender para 18, mas o sistema começa a esquentar, e então u cresce e depois decresce novamente tendendo para 18.

Resposta

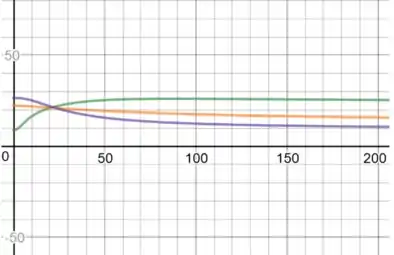
  1. u ( t , x ) = 30 - x + ∑ n = 1 ∞ 60 n ³ π ³ [ 2 ( 1 - c o s ( n π ) ) - n ² π ² ( 1 + c o s ( n π ) ) ] e n ² π ² t 900 s e n ( n π x 30 )

  3. u versus t para x=12. Podemos ver que u decresce, depois cresce um pouco, e finalmente decresce até chegar a um valor constante. Quando x=12, u começa a partir de u ( 12,0 ) = 12 ( 60 - 12 ) 30 = 19.2 e tende para 30 - 12 = 18 .

Fisicamente, u começa a tender para 18, mas o sistema começa a esquentar, e então u cresce e depois decresce novamente tendendo para 18.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que as extremidades de uma barra de cobre com 100 cm de comprimento são mantidas a 0°C. Suponha que o centro da barra é aquecido a 100°C por uma fonte externa de calor; que essa situação se ma
Considere uma barra com 40 cm de comprimento cuja temperatura inicial é dada por u ( x , 0 ) = x ( 60 - x ) / 30 . Suponha que α 2 = 1 / 4 c m 2 / s e que ambas as extremidades da barra estão isoladas
Considere uma barra de alumínio, com 20 cm de comprimento, inicialmente a uma temperatura uniforme de 25°C. Suponha que, no instante t = 0, a extremidade x = 0 é esfriada a 0°C, enquanto a extremidade
Escreva u(x, t) = υ(x) + (x, t), em que υ e são as partes estacionária e transiente,respectivamente, da solução. Enuncie os problemas de valores de contorno que υ(x) e w(x, t)satisfazem, respectivamen
Suponha que α 2 = 1 e que s(x) = k na Eq. (i), com k constante. Encontre υ(x).Suponha que T 1 = 0 ,T 2 = 0 ,L = 20 ,k = 1 / 5 e que f(x) = 0 para 0