Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 9

Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se ela for convergente, calcule a soma. Se for divergente, explique por quê.

∑ n = 1 ∞ 12 - 5 n

Passo 1

Hey, pessoal!

Nossa questão quer que a gente encontre as 10 primeiras somas da série e que a gente defina sua convergência ou divergência, além de fazer o gráfico. Para calcular os termos da soma da série podemos usar:

s n = a n + s n - 1

Com n = 1,2 , 3 , … , 10 .

Vamos dar uma olhada na nossa série:

∑ n = 1 ∞ 12 - 5 n

Sempre que temos termos exponenciais na nossa série podemos “desconfiar” que pode se tratar de uma série geométrica. A série geométrica tem uma análise de soma e de convergência bem simples, então isso facilitaria nossa vida. Caso não se lembre, ela tem esse formato aqui:

∑ n = 1 ∞ a r n - 1

Esse tipo de série converge se r < 1 .

Séries geométricas tem expressão pronta para cálculo da soma:

s n = a 1 - r

Então essa será nossa expressão para a soma.

Passo 2

Vamos reescrever nossa série como uma série geométrica. Vamos tirar o 12 “para fora” da nossa fração e ficaremos com:

∑ n = 1 ∞ 12 - 5 n = ∑ n = 1 ∞ 12 - 1 5 n

Dessa forma termos uma série geométrica com razão igual a r = - 1 5 .

Passo 3

Bora calcular as primeiras dez somas parciais da série? Usaremos:

s n = a n + s n - 1

Para n = 1 :

S 1 = a 1 = 12 - 5 1 = - 12 5 = - 2,40000

Para n = 2 :

S 2 = a 1 + a 2 = - 2,4 + 12 - 5 2 = - 1,92000

Para n = 3 :

S 3 = a 1 + a 2 + a 3 = S 2 + a 3 = - 1,92 + 12 - 5 3 = - 2,01600

Para n = 4 :

S 4 = S 3 + a 4 = - 2,016 + 12 - 5 4 = - 1,99680

Metade do caminho! Para n = 5

S 5 = - 2,00064

Para n = 6 :

S 6 = - 1,99987

Para n = 7 :

S 7 = - 2,00003

Para n = 8 :

S 8 = - 1,99999

Para n = 9 :

S 9 = - 2,00000

Para finalizar, para n = 10 :

S 10 = - 2,00000

Também podemos colocar o valor de algum dos termos da sequência que irão aparecer no gráfico.

Para n = 1 :

a 1 = 12 - 5 1 = - 12 5

Para n = 2 :

a 2 = 12 - 5 2 = 12 25

Para n = 3

a 3 = 12 - 5 3 = - 12 125

E assim sucessivamente.

Passo 4

Show! Agora vamos fazer o gráfico da sequência de termos a 1 , a 2 , … e o gráfico da sequência de somas parciais S 1 , S 2 ,   … :

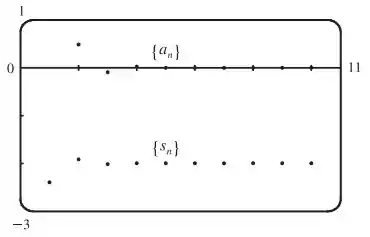
Olhando pro gráfico da sequência de termos, ele parece convergir pra 0 , que seria uma condição necessária (mas não suficiente) pra série convergir.

E se a gente olhar pro gráfico da sequência de somas parciais, ele parece convergir pra - 2 , então parece que a série é convergente com soma - 2 . Será mesmo?

Passo 5

Pra confirmar nossa observação do gráfico, vamos calcular a soma da série:

∑ n = 1 ∞ 12 - 5 n = ∑ n = 1 ∞ 12 - 1 5 n

Olha só, isso é a soma infinita de uma progressão geométrica com r = - 1 5 < 1 . O primeiro termo é a 1 = - 12 5 , então:

∑ n = 1 ∞ 12 - 5 n = a 1 1 - r = - 12 5 1 - - 1 5

Fazendo a subtração de frações no denominador:

∑ n = 1 ∞ 12 - 5 n = - 12 5 6 5 = - 12   .   5 5   .   6

Simplificando:

∑ n = 1 ∞ 12 - 5 n = - 12   .   5 5   .   6 = - 2

Como havíamos previsto, né?

Resposta

A Série é convergente e sua soma é:

∑ n = 1 ∞ 12 - 5 n = - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o comando de frações parciais em seu SCA para encontrar uma expressão conveniente para a soma parcial; então utilize essa expressão para encontrar a soma da série. Verifique sua resposta usando o
Trace as curvasy = x n ,0 ≤ x ≤ 1 , para n = 0 ,1 ,2 ,3 ,4 , … na mesma tela. Encontrando as áreas entre as curvas sucessivas, dê uma demonstração geométrica do fato, mostrado no Exemplo 6, de que ∑ n
O que está errado com o seguinte cálculo?0 = 0 + 0 + 0 + ... = (1 - 1) + (1 - 1) + (1 - 1) + ... = 1 - 1 + 1 - 1 + 1 - 1 + ... = 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1) + ... = 1 + 0 + 0 + 0 + ... = 1
Se a n -ésima soma parcial de uma série ∑ n = 1 ∞ a n for s n = 3 - n 2 - n Encontre a n e ∑ n = 1 ∞ a n .
A figura exibe dois círculos C e D de raio 1 que se tocam em P . T é uma reta tangente comum; C 1 é o circulo que toca C , D e T ; C 2 é o circulo que toca C , D e C 1 ; C 3 é o circulo que toca C , D