Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 79
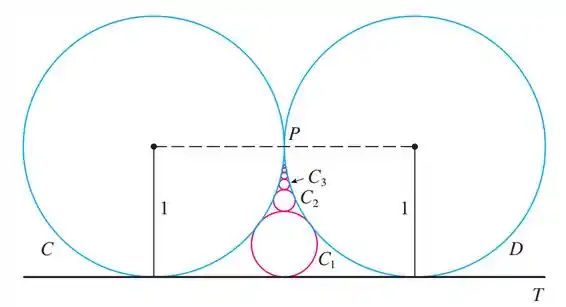
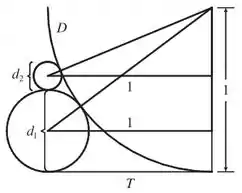
A figura exibe dois círculos e de raio que se tocam em . é uma reta tangente comum; é o circulo que toca , e ; é o circulo que toca , e ; é o circulo que toca , e . Esse procedimento pode continuar indefinidamente e produzir uma sequência infinita de círculos . Encontre uma expressão para o diâmetro de e então forneça outra demonstração geométrica do Exemplo 8
Passo 1
Fala aí pessoal!
Para resolver essa questão precisamos achar alguma relação que nos dê os diâmetros dos círculos . Para isso, vamos criar outra sequência onde é o diâmetro de , e para calcular vamos traçar uma do centro do círculo até o centro de e outra reta paralela a , formando triângulos retos
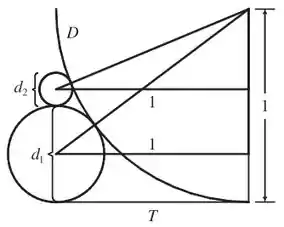
Assim podemos aplicar o Teorema de Pitágoras nos triângulos e calcular os diâmetros dos círculos rosas. Nós vamos calcular , e e tentar encontrar um padrão pra definir o valor de .
Passo 2
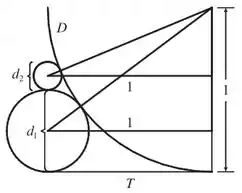
Perceba que a hipotenusa vai ser sempre o raio de que é mais o raio de que é , a base do triangulo vai ser sempre e a altura vai ser menos e menos ainda a soma de todos os diâmetros anteriores.
Pro primeiro triângulo:
Subtraindo dos dois lados
Temos agora uma diferença de quadrados do lado esquerdo, onde
Passo 3
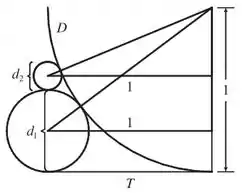
Agora vamos calcular . Para o segundo triângulo:
Fazendo o mesmo procedimento
Abrindo a soma de quadrados:
Substituindo o valor de :
E assim achamos o :
Passo 4
Calculando agora
Abrindo a diferença de quadrados:
Substituindo os valores de e :
Manipulando a expressão:
Encontramos
Passo 5
Vamos olhar o que achamos:
No numerador sempre temos 1. No denominador temos multiplicado pelo inteiro consecutivo.
Conseguimos achar um padrão!
Passo 6
Voltando a imagem percebemos que os círculos vao diminuindo e eles tem um limite que não podem ultrapassar, pois as circunferências e se tocam no ponto , e se analisarmos bem quando , , como assim? Quanto maior o menor o diâmetro e quando o diâmetro tende a zero, a circunferência vira um ponto e isso só ocorre no limite quando as circunferências estão próximas o suficiente de .
O que tiramos disso? Como o limite é , podemos dizer que a soma de todos os diâmetros é igual a distancia de e , que é o raio de , logo temos que