Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 48
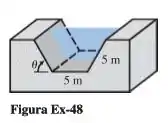
Um canal de drenagem deve ser feito de tal forma que a secção transversal é um trapézio com os lados igualmente inclinados (Figura Ex-48). Se os lados e a base tiverem um comprimento de , como escolher o ângulo , de forma que a área da secção transversal do canal seja máxima?
Passo 1
Então pessoal, o que devemos fazer aqui, pelo menos inicialmente, é escrever as variáveis do nosso problema em termos de . Da imagem que nos foi dada conseguimos tirar o seguinte, saca só:
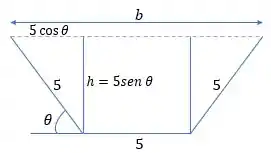
Aqui vale ressaltar que as funções trigonométricas aparecem por conta da decomposição da hipotenusa do triângulo retângulo formado, ok? Show! A área de um trapézio é dada da seguinte forma:
No qual é a base maior, é a base menor e é a altura do trapézio. De acordo com a figura que desenhamos:
Substituindo na nossa expressão, teremos:
Passo 2
Como queremos a maior área possível para o trapézio, então estamos falando de ponto de máximo. Sendo assim, vamos em busca desse ponto de máximo! Derivando nossa função, teremos:
Como , então:
Igualando nossa derivada a zero:
As únicas possibilidades disso dar zero são se:
Ou:
Da primeira tiramos que , então . Já da segunda tiramos que , então . No entanto, o nosso intervalo está contido em , pois é a validade das componentes de seno e cosseno que escrevemos! Sendo assim, o único ponto crítico é , além das extremidades do intervalo!
Passo 3
Agora que encontramos o ponto crítico, vamos substitui-lo na nossa expressão da área:
Mas como sabemos que essa é a maior área? Bom, para termos certeza vamos substituir as extremidades na nossa expressão também, se liga:
Sendo assim, podemos concluir que, de fato, a maior área é , no qual o ângulo associado é !