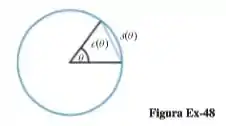
48-Um ângulo central que mede radianos subentende uma coordenada de comprimento e um arco circular de comprimento no círculo da figura abaixo. Usando sua intuição, qual seria a conjectura sobre o valor de ? Verifique sua conjectura calculando o limite.

Gente, a única forma de resolvermos o limite acima é utilizando o limite trigonométrico fundamental:

Maxxx o nosso limite está um pouco diferente do que deveria ser, né ?

Então, vamos ajustar esse limite. Dividindo o numerador e o denominador por 2, nós não alteramos a fração e fazemos com que o denominador fique igual ao argumento do seno.

Assim,

Fim!