A cidade de Nova Delhi, na Índia, está localizada a uma latitude de . Use a Figura para encontrar uma função que modele o número de horas de luz solar em Nova Delhi como uma função da época do ano. Para verificar a precisão do seu modelo, use o fato de que nessa cidade, em de março, o Sol surge às da manhã e se põe às .
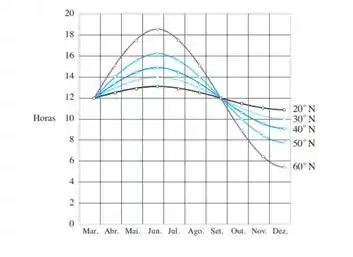
Passo 1
Fala galera, beleza? Essa questão aqui é sobre transformação de gráficos! Ta preparado? Bora meter ficha então! Nosso primeiro passo é identificar quem vai ser a nossa função modelo.
Dando uma olhada na Figura que a questão nos dá, é possível perceber que os gráficos desenhados lembram um pouco uma senóide, o gráfico da função seno. Da uma olhada em uma senóide caso não estejas mlembrando como ela é:
A diferença é que o gráfico que temos no enunciado (referente à ) está deformado e deslocado com relação ao gráfico de uma senóide, então vamos ter que encontrar os parâmetros que descrevem a nossa curva! A curva mais geral possível de uma senóide é da seguinte forma:
Na nossa função, será a a quantidade de luz solar em horas, o tempo em dias, o deslocamento na vertical, o fator de deformação na vertical, o fator de deformação na horizontal e o deslocamento na horizontal, beleza?
Passo 2
Agora, nós iremos verificar o deslocamento vertcal da curva. É possível perceber que ela se encontra unidades acima do eixo , que é onde a função fica. Logo, nossa função está deslocada unidades para cima, ou seja, teremos que .
Passo 3
Para acharmos a deformação na vertical, temos que verificar a amplitudeda função. Uma função seno normal tem amplitude (atinge um máximo valor em e um mínimo valor em ). Para acharmos a amplitude do nosso gráfico, temos que tirar a diferença entre o maior e o menor valor da função e dividir por .
O maior valor é e o menor valor é . Fazendo as contas:
Sendo assim, acabamos de descobrir que o nosso , beleza?
Passo 4
Para achar a deformação na horizontal, temos que pensar no período da função seno (já deu para perceber que essa é quase puramente sobre função seno, né? Ela aparece que só em Cálculo lá na frente, então qualquer coisa dá uma revisada para ficar com ela na ponta da língua!).
O período de uma função seno é . O nosso gráfico atua sobre os dias no ano: como temos dias no ano, esse deve ser o período do nosso modelo.
Para achar o nosso fator de deformação na horizontal temos que, então, dividir por (o período da senóide normal pelo período da senóide que a gente quer). Ou seja, teremos que .
Passo 5
Esse é o último número que precisamos, o deslocamento horizontal ! O gráfico começa em de março, que é o dia do ano. Logo, o nosso gráfico tem que ficar unidades para a direita com relação a função seno normal. Teremos então que (o sinal de menos desloca para a direita, beleza? Se fosse positivo, o deslocamento seria para a esquerda).
Passo 6
Temos todos os valores que procurávamos! O nosso modelo vai ficar assim:
O enunciado fala para a gente testar o modelo para um intervalo de tempo de até , o que vai dar um tempo de . Temos que transforar esse de minutos para horas e, para isso, dividimos por :
Logo, nosso intervalo de tempo de luz do dia é de horas. Esse é o tempo de luz do dia que de fato se tem na cidade, agora nós temos que achar o tempo que o nosso modelo fornece!
Como, de acordo com o enunciado, estamos lidando com o dia de março, que é o dia do ano, teremos . Jogando na nossa função:
O seno de é, aproximadamente, . Substituindo:
Pronto, achamos a quantidade de luz solar pelo nosso modelo!
Passo 7
Calma que ta acabando, esse é o nosso último passo! Vamos comparar o valor do modelo com o valor real . Para fazer isso nós calculamos o erro percentual, dado pela seguinte expressão:
Substituindo os valores, a gente vai ter:
O nosso erro percentual deu menos que , ou seja, a precisão do nosso modelo é excelente!
Pronto, terminamos a questão! Ela é meio longa mas sabendo direitinho como funciona a função seno e prestando atenção no gráfico, é só fazer com calma que sai ;)
Resposta
A função modelo é:
E a sua precisão é muito boa, tendo um erro menor que com relação aos valores reais.