Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.9 - Ex. 13b
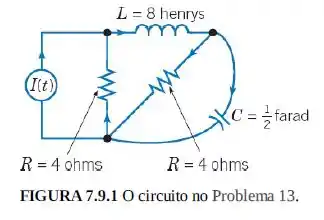
O circuito elétrico mostrado na Figura 7.9.1 é descrito pelo sistema de equações diferenciais
Em que é a corrente através do indutor, é a queda de tensão através do capacitor, e é a corrente fornecida pela fonte externa.
(a) Determine uma matriz fundamental para o sistema homogêneo associado à Eq. (i). Veja
o Problema 25 da Seção 7.6.
(b) Se, determine a solução do sistema (i) que satisfaz a condição inicial.
Passo 1
Para encontrar uma solução para o problema inicial, nós iremos aplicar o método da variação de parâmetros . Desde que nós possuamos a matriz fundamental, coisa que nós já determinamos não é mesmo, então vamos prosseguir.
Antes de tudo temos que terminar a matriz inversa da matriz fundamental, pois,
E a solução final é , então vamos prosseguir:
Temos que a matriz fundamental é:
Determinado a matriz inversa da matriz fundamental:
Passo 2
Como temos e a matriz inversa da matriz fundamental, vamos determinar :
Efetuando os produtos:
Integrando temos:
Passo 3
Possuímos a matriz fundamental acabamos de terminar , podemos determinar a solução final não homogênea do sistema:
Efetuando a multiplicação temos:
Finalmente podemos determinar a solução do valor inicial: