Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 44
Cissoide de Diocles (de cerca de 200 a.C.): Determine as equações para a tangente e a normal à cissoide de Diocles em .
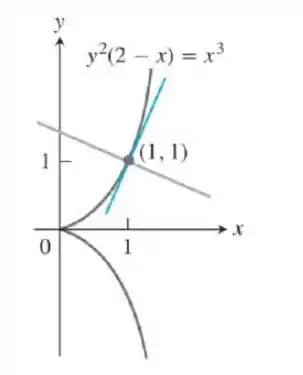
Passo 1
Questões de derivação implícita parecem ser difíceis, mas no final são tão simples quanto quaisquer outras questões de derivadas! Vamos destrinchar trecho por trecho desta questão.
Esta questão nos pede para determinar duas retas, uma tangente e uma normal a curva no ponto . Seja uma reta tangente ao ponto :
A reta normal a curva neste mesmo ponto é:
E, os coeficientes angulares de ambas as retas respeitam a seguinte relação matemática:
E agora, aparece um questionamento. Como determinaremos o coeficiente angular de qualquer uma dessas duas retas? Para isto, usaremos o nosso conhecimento de derivadas, e em especial, derivação implícita. A derivada de uma função nos dá o coeficiente angular de uma reta tangente a curva. Consequentemente, se substituirmos as coordenadas do ponto , obteremos o coeficiente angular da reta tangente a curva neste ponto. A partir deste coeficiente, conseguimos obter facilmente o coeficiente da reta normal e compor ambas as retas.
Sendo assim, vamos a nossa questão.
Passo 2
Vamos começar por derivar a nossa função implicitamente. Sendo assim, temos:
Passo 3
Para obter o coeficiente angular da reta tangente, basta substituir e na função descoberta no passo anterior. Assim, temos:
Portanto,
Passo 4
Agora que obtemos o coeficiente angular da reta tangente, para obter o da reta normal, basta utilizar seguinte relação:
Passo 5
Vamos obter agora a equação da reta tangente. Desta forma, temos:
Passo 6
Já para a equação da reta normal, temos:
Resposta
A equação da reta tangente a curva é:
Já a equação da reta normal, é dada por: