Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 62

Classifique as funções cujos gráficos estão nas figuras a seguir como pares, ímpares ou nenhum desses casos:

(a)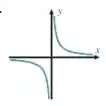

(b)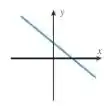

Passo 1

Antes de tudo, vamos relembrar qual a relação entre funções ímpares/pares e as simetrias!

Bem, para ser par, por definição, deve haver uma simetria em relação ao eixo , já que:

E, para ser ímpar, também por definição, deve haver uma simetria em relação à origem, certo? Isso porque:

E, para ser simétrico em relação à alguma coisa, o gráfico deve se refletir em relação à essa coisa. Como um espelho mesmo! Veremos melhor na prática.

Passo 2

(a) Agora, vamos olhar para o gráfico e identificar alguma simetria:

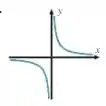
Consegue ver que temos um valor para a função para um positivo e o oposto desse valor para um mesmo , só que negativo? Nesse caso, uma parte da função se torna o espelho de outra parte, através da origem!! Uma parte da função é gerada espelhando a outra pela origem!

Como temos uma reflexão pela origem:

E, assim, essa é uma função ímpar.

Passo 3

(b) Vamos olhar para o gráfico e identificar alguma simetria:

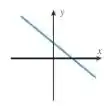
Bom, temos alguma parte espelhada? Pela origem, não, pois só temos um lado da origem com valores. Por , também não, pois a parte em cima do não se repete abaixo dele. E por , mais uma vez não temos, pois a parte à direita não é igual à parte pela esquerda de .