Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 60
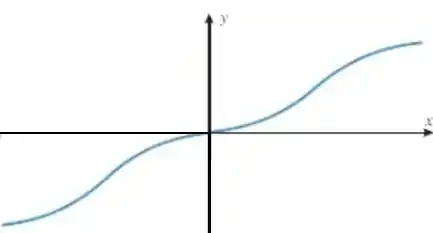
A figura abaixo mostra uma parte de um gráfico de uma função . Complete o gráfico supondo que
(a) é uma função par
(b) é uma função ímpar
Passo 1
Bem, para ser par, por definição, deve haver uma simetria em relação ao eixo , já que:
E, para ser ímpar, também por definição, deve haver uma simetria em relação à origem, certo? Isso porque:
E, para ser simétrico em relação à alguma coisa, o gráfico deve se refletir em relação à essa coisa. Como um espelho mesmo! Veremos melhor na prática.
Passo 2
(a) Nesse caso, devemos olhar para o reflexo do gráfico pelo eixo :
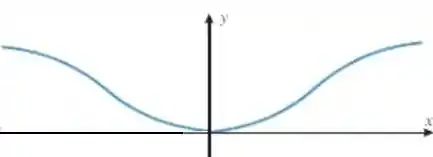
Só espelhar a função pelo eixo .
Passo 3
(b) Nesse caso, devemos olhar para o reflexo do gráfico pela origem:
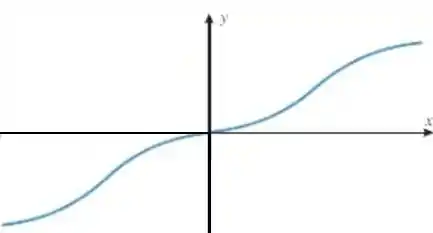
Só espelhar a função pela origem.
Resposta
(a)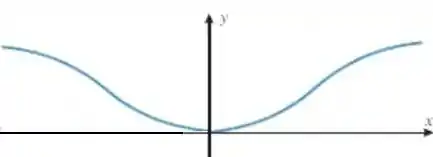 
(b) 
Exercícios de Livros Relacionados
Se f e g são funções pares, f + g é par? Se f e g são funções impares , f + g é impar? O que se pode dizer se f for par e g for ímpar ?
Se f e g são funções pares, o produto é par? Se f e g são funções ímpares, f g é ímpar? O que se pode dizer se f for par e g for ímpar? Justifique suas respostas.
Determine se f é par, ímpar ou nenhum dos dois. Se f for par ou ímpar, use a simetria para esboçar seu gráfico. f x = x 4 - 4 x 2
Determine se f é par, ímpar ou nenhum dos dois. Se f for par ou ímpar, use a simetria para esboçar seu gráfico. f x = 3 x 3 + 2 x 2 + 1
Determine se f é par, ímpar ou nenhum dos dois. Se f for par ou ímpar, use a simetria para esboçar seu gráfico. f x = x 2 + x