Determine se é par, ímpar ou nenhum dos dois. Se for par ou ímpar, use a simetria para esboçar seu gráfico.
Passo 1
Desejamos saber se a nossa função é par, ímpar ou nenhuma das duas coisas, mas caso seja um dos dois casos devemos esboçar seu gráfico. Assim, devemos lembrar primeiramente o que é uma função par ou ímpar e que simetria é essa que essas funções apresentam.
- Uma função é chamada de função par quando: . O gráfico desse tipo de função é simétrico em relação ao eixo .
- Uma função é chama de função ímpar quando: . O gráfico desse tipo de função apresenta simetria em relação à origem.
Passo 2
Como já temos o valor de precisaremos apenas calcular o substituindo na expressão da função onde tem por . Assim, vamos ter
Então a função é par e seu gráfico é dado por
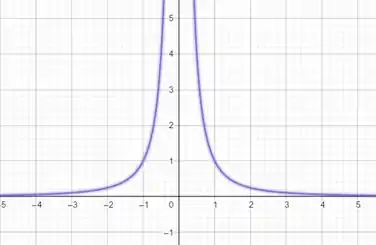
Resposta