Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 57
Classifique em pares, ímpares ou nenhuma dessas as unções cujos valores estão dados na tabela a seguir.
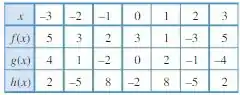
Passo 1
Antes de classificar, precisamos relembrar o que são funções pares e ímpares.
Uma função é par quando:
E uma função é ímpar quando:
Então, vamos analisar se as funções entram em algum desses critérios ou não. Ok?
Passo 2
Olhando para a tabela:
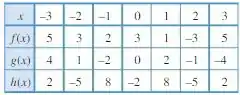
Vamos começar com . Primeiro, vamos ver se ela é par, então queremos que para qualquer ponto . Se um ponto não bater com essa sentença, já é o suficiente para ela não ser par.
Temos que , então, para ser par . E isso acontece, logo, já verificamos 2 pontos!
Temos que , então, para ser par . E isso acontece não acontece!! Temos que .
E como já vimos que , já sabemos que ela também não será ímpar!! Pois esse ponto já não se encaixa no critério de .
Passo 3
Agora . Primeiro, vamos ver se ela é par, então queremos que para qualquer ponto . Se um ponto não bater com essa sentença, já é o suficiente para ela não ser par.
Temos que , então, para ser par . E isso acontece não acontece!! Temos que .
Logo, ela não é par! Vamos ver se ela é ímpar, ou seja, se para todo ponto.
Temos que , então, para ser ímpar . E isso acontece acontece! Já foram 2 pontos.
Temos que , então, para ser ímpar . E isso acontece acontece!
Temos que , então, para ser ímpar . E isso acontece acontece!
Opa, ela se encaixou no critério para ser ímpar!!
Obs.: Não precisamos ver o valor para , pois não tem oposto. E estamos sempre olhar para o par e .
Passo 4
Agora . Primeiro, vamos ver se ela é par, então queremos que para qualquer ponto . Se um ponto não bater com essa sentença, já é o suficiente para ela não ser par.
Temos que , então, para ser par . E isso acontece acontece!
Temos que , então, para ser par . E isso acontece acontece!
Temos que , então, para ser par . E isso acontece acontece!
Opa, ela se encaixou no critério para ser par!!
Resposta
é nenhuma das duas.
é ímpar.
é par.