Coloque num gráfico o ponto com coordenadas polares . Ache outro conjunto de coordenadas polares para esse ponto sendo (a) e ; (b) e; (c)
Passo 1
Bom, primeiro colocaremos o ponto no gráfico:
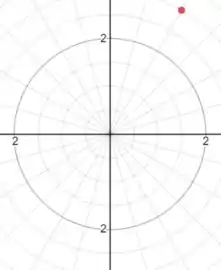
Passo 2
E agora vamos identificar as condições dadas em cada letra, para que possamos manter o ponto, mesmo mudando suas coordenadas. Na letra (a) a coordenada precisa ter então determinamos e ajustamos o ângulo conforme as condições, de maneira a ficar no mesmo ponto. Como rotacionamos em o r, vamos somar ao valor dado
E agora ajustamos à condição da letra (a), em ângulos, uma rotação de seria o mesmo que fazermos .
Logo, as coordenadas serão:
Passo 3
Na letra (b) faremos a mesma coisa com r, vamos escrevê-lo como por causa da condição . Como rotacionamos novamente em o r, nosso então ficará:
E isso já satisfaz a condição , então nossas coordenadas serão:
Passo 4
E na letra (c) não mexeremos em r, mas precisaremos ajustar o ângulo de maneira a manter a posição de r no mesmo ponto, com isso precisamos somar para atingir a condição
E as coordenadas então serão: