Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 15
Nos Exercícios 13 a 20, o gráfico da equação dada é uma elipse ou uma hipérbole. Ache o centro, vértices e focos da cônica. Se o gráfico for uma elipse, ache também as extremidades do eixo menor. Se o gráfico for uma hipérbole, ache também as equações das assíntotas. Faça um esboço da curva e mostre os focos. Se a curva for uma hipérbole, trace também as assíntotas.
15.
Passo 1
Então pessoal, de ínicio temos que saber qual é o formato de uma equação de elipse e de hipérbole para podermos comparar com a equação que nos foi dada, certo? Temos que:
Para a equação que nos foi dada, temos:
Que é uma equação de hipérbole!
Passo 2
Agora que já sabemos que tipo de cônica a nossa equação se trata, vamos descobrir seu centro, vértices, focos e extremidades do eixo menor.
Centro:
Vértices: e
Para determinarmos a distância do centro aos focos, temos que utilizar a relação:
No qual é a distância supracitada. Sabendo que e , temos:
Focos: e
Por fim, para determinarmos as equações das assíntotas, temos que utilizar as relações:
Substituindo os valores, teremos:
Esboçando essa hipérbole, teremos o seguinte, galera:
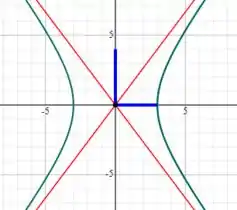
Resposta
Centro:
Vértices: e
Focos: e
Assíntotas:
