Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 86
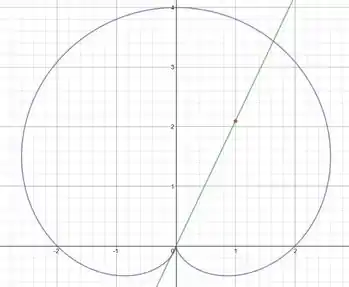
Para a curva , ache X e no ponto (1, . Faça um esboço da curva mostrando X e .
Passo 1
Para essa questão, temos que X e correspondem respectivamente a reta que toca o ponto indicado e a reta tangente a nossa curva horizontalmente. Portanto, vamos para o esboço.
Passo 2
Para a nossa reta tangente, podemos derivar a nossa equação e igualar a 0 no ponto indicado pelas coordenadas da questão.
Passo 3
Portanto, vamos ao esboço com a reta indicada:
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Coloque num gráfico o ponto com coordenadas polares - 3 ,- 2 3 π . Ache outro conjunto de coordenadas polares para esse ponto sendo (a) r0 e 0 ≤ θ2 π ; (b) r0 e - 2 π ≤ θ0 ; (c) r0e2 π ≤ θ4 π
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(c) ( - 4 ,2 3 π )
Nos exercícios 21 e 22, ache as coordenadas cartesianas retangulares dos pontos cujas coordenadas polares são dadas21(d) ( - 1 ,7 6 π )