Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 18
Combinando os resultados dos Problemas 16 e 17, mostre que a solução do problema
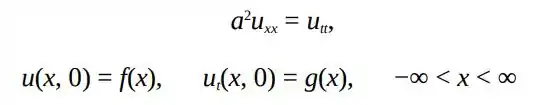
é dada por
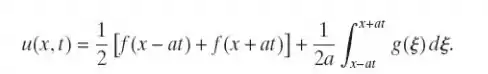
Passo 1
Pela 16 vemos que o resultado é dado por:
Com equação de onde
Cujas condições iniciais são com
E pela que:
Com equação de onda
Cujas condições iniciais são:
com
Então se fizermos . Uma vez que a EDO é linear nós podemos dizer que a soma das duas ondas lineares satisfaz a equação com condições iniciais iguais a:
Então é uma solução geral para a propagação de onda descrita.
Resposta
Explicação do passo 1
Exercícios de Livros Relacionados
Os Problemas 19 e 20 indicam como é possível mostrar que a solução formal (20), (22) das Eqs. (1), (3) e (9) é, de fato, a solução desse problema.19- Usando a identidade trigonométrica s e nAc o sB=½
O movimento de uma membrana circular elástica, como a membrana de um tambor, é determinado pela equação de onda bidimensional em coordenadas polaresSupondo que u ( r ,θ ,t )=R r Θ ( θ ) T ( t ) , enco
Seja h ( ξ ) o deslocamento inicial em [ 0 ,L ] estendido a ( - L ,0 ) como uma função ímpar e estendido ao resto da reta como uma função periódica de período 2 L . Supondo a continuidade de h e suas
Considere a equação de onda a 2 u x x = u t t em um meio unidimensional infinito, sujeita às condições iniciaisUsando a forma da solução obtida no Problema 13, mostre queUse a primeira das equações no
Considere uma corda elástica de comprimento L cujas extremidades são mantidas fixas. A corda écolocada em movimento a partir da sua posição de equilíbrio, com velocidade inicial ut(x, 0) = g(x). Em ca