Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 21
O movimento de uma membrana circular elástica, como a membrana de um tambor, é determinado pela equação de onda bidimensional em coordenadas polares
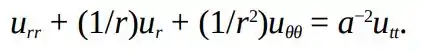
Supondo que , encontre as equações diferenciais ordinárias satisfeitas por .
Passo 1
Bem, vamos derivar a equação de em e
Substituindo isso na equação diferencial dada nós teremos:
Escrevendo de outra forma:
Dividindo tudo por teremos:
Passo 2
Aplicando as relações:
O intuito aqui é sumir com tudo que não for e nem
Note que o valor é e não
Nós teremos:
O que nos dará:
Além de:
Resposta
Exercícios de Livros Relacionados
Um fio de aço com 5 pés (em torno de 1,5 m) é esticado por uma tensão de 50 lb (em torno de 222 newtons). O fio tem densidade de massa de 0,026 lb/pé (em torno de 0,034 kg/m).Encontre a velocidade de
Podem ser introduzidas variáveis adimensionais na equação de onda a 2 u x x = u t t da seguinte maneira:Seja s = x L e mostre que a equação de onda fica a 2 u s s = L 2 u t t Mostre que L a tem dimens
Considere uma corda elástica de comprimento L cujas extremidades são mantidas fixas. A corda écolocada em movimento a partir da sua posição de equilíbrio, com velocidade inicial ut(x, 0) = g(x). Em ca
Suponha que a corda no Problema 10 começa a partir da posição inicial f ( x ) = 8 x ( L - x 2 ) / L 3 . Siga as instruções no Problema 10 para esse novo problema.
Se uma corda elástica tiver uma extremidade solta, a condição de contorno a ser satisfeita aí será u x = 0 . Encontre o deslocamento u(x, t) de uma corda elástica de comprimento L, fixa em x = 0 e sol