Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.8 - Ex. 37
Um cometa move-se numa órbita parabólica em torno do Sol, no foco da parábola. Quando o cometa está a milhões de quilômetros do Sol, o segmento de reta do cometa ao Sol faz um ângulo de rad com o eixo da órbita. (a) Ache a equação da órbita do cometa. (b) Qual a distância mínima entre o cometa e o Sol?
Passo 1
A questão diz que a órbita de um cometa é parabólica e que quando o cometa está a milhões de km do Sol, o ângulo que ele faz com o eixo principal da parábola é . Usando uma escala de unidades em milhões de km, temos o seguinte esquema:
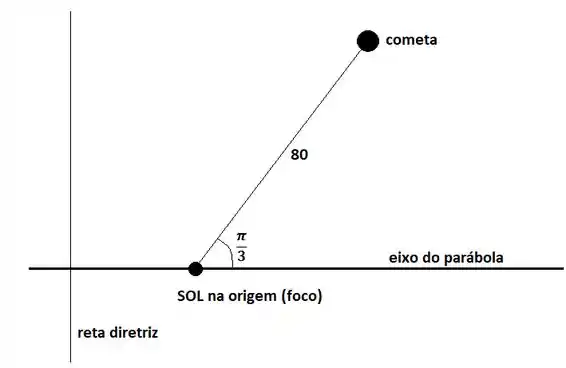
Posicionamos o Sol (foco) na origem e a reta diretriz à sua direita. Nessa situação, a equação geral das cônicas em coordenadas polares é:
Como se trata de uma parábola, temos que , de modo que
A questão faz duas perguntas: qual a equação da órbita (só falta achar ) e qual a distância mínima do cometa ao Sol na órbita.
Passo 2
Para o item (a), queremos a equação da parábola. Portanto, precisamos achar . Note que quando , temos que . Assim,
Assim, a equação da órbita é
*As unidades dessa equação são milhões de km.
Passo 3
Para o item (b) nós devemos achar a menor distância que o cometa fica do Sol. Isso ocorre em :
Assim, a distância mínima do cometa ao Sol são milhões de quilômetros.
Resposta
(a)
(b) milhões de km.