Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 35
As figuras a seguir mostram os gráficos de e de , conforme são exibidos por uma calculadora gráfica TI-83.
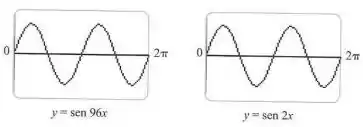
O primeiro gráficos é inexato. Explique por que os dois gráficos parecem ser idênticos.
Passo 1
Pessoal, vamos lá! Não se assusta com essa questão!
Ela nos dá 2 funções diferentes que tem o mesmo gráfico quando usadas com uma calculadora específica. E nos pergunta porque isso acontece.
Esse problema é mais técnico e envolve o funcionamento de calculadoras gráficas. No caso, a janela da calculadora TI-83 é de pixels de largura. E isso vai definir quantos pontos de cada função vamos conseguir marcar.
Como queremos plotar o gráficos no intervalo . Considerando o primento ponto marcado como e o último como , existirão intervalos entre pontos marcados pela calculadora. O tamanho desses intervalos será
Assim, os valores plotados pela calculadora serão nos pontos
Isso pras 2 funções tá!
No passo 2 vamos analisar o que acontece nesses pontos plotados pelas 2 calculadoras que faz com que os gráficos sejam iguais.
Passo 2
Quando plotamos , os pontos plotados são:
Já para , os pontos são
Mas veja bem, os valores da segunda função podem ser reescritos dessa forma:
Agora vamos pegar essa relação aqui que vale pra arcos côngruos. Se a gente pega um ângulo e adiona um número inteiro de voltas no ciclo trigonométrico, o seno vai ser igual
Sendo assim:
E finalmente!
Ou seja, nos pontos que a calculadora marca, as duas funções são iguais. Isso não significa que elas são iguais em todos os pontos, mas nesses elas são. Assim, por coincidência, os pontos marcados para serão os mesmos que para .
Concluindo, o gráfico da esquerda é impreciso: ele marca alguns pontos que coincidem exatamente com uma outra função. Nos demais pontos, onde as funções não coincidem, a calculadora não marca.
Resposta
Devido à resolução da tela da calculadora (número de pixels), são marcados apenas os pontos que as 2 funções tem em comum, fazendo com que eles pareçam iguais. Os pontos diferentes não foram marcados.