Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.1 - Ex. 20
Considere o circuito ilustrado na figura a seguir.
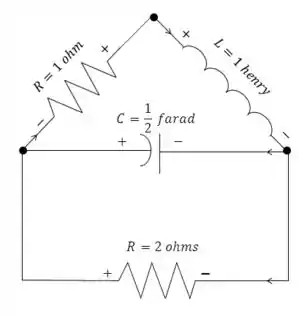
Use o método esboçado no problema 19 para mostrar que a corrente através do indutor e a diferença de tensão através do capacitor satisfazem o sistema de equações diferenciais
Passo 1
Antes de tudo vamos contextualizar. O problema 19 pede para obtermos um sistema de equações diferenciais para um circuito RLC paralelo. Para isso, seguimos os seguintes passos:
Aplicar a segunda lei de Kirchhoff nos dois laços do circuito para obter as relações entre as quedas de tensão em cada componente; aplicar a primeira lei de Kirchhoff para chegar em uma relação para as correntes que atravessam cada componente; usar as equações características de tensão/corrente para cada componente; combinar as equações para encontrar o sistema que foi pedido.
Com base neste método vamos tentar chegar ao sistema de equações:
Vamos lá???
Passo 2
Vamos começar chamando algumas variáveis: , , e são as quedas de tensão no capacitor, no resistor de 1 ohm, no resistor de 2 ohms e no indutor, respectivamente. Da mesma forma, , , e são as correntes correspondentes. Então, no final devemos chegar ao sistema:
Agora, vamos ao método. Nosso primeiro passo será aplicar a segunda lei de Kirchhoff no primeiro laço:
Como a corrente (em azul) atravessa o capacitor, o resistor de 1 ohm e o indutor na direção negativo-positivo, as tensões , e são positivas. Além disso, como não temos fontes de tensão no laço a somatória das tensões é zero. Então:
Vamos agora para o segundo laço:
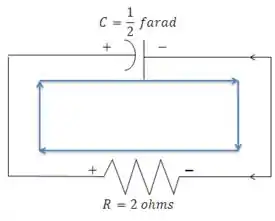
Como a corrente (em azul) atravessa o resistor de 2 ohms na direção negativo-positivo, a tensão é positiva. Da mesma forma, como a corrente passa pelo capacitor na direção positivo-negativo a tensão é negativa. Além disso, como não temos fontes de tensão no laço a somatória das tensões é zero. Então:
O próximo passo é aplicarmos a primeira Lei de Kirchhoff no circuito. Ela diz que a somatória das correntes que saem do nó é igual à soma das correntes que entram no nó. Vamos usar o seguinte nó para aplicar a lei:
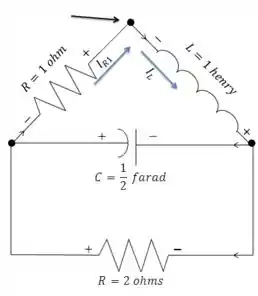
Podemos ver que o nó que escolhemos possui uma corrente saindo e uma corrente entrando no nó. Então:
Pela primeira Lei de Kirchhoff:
Vamos aplicar novamente a primeira lei de Kirchhoff para outro nó:
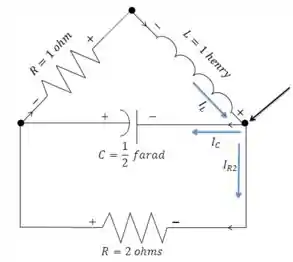
Podemos ver que este nó possui duas correntes saindo e uma corrente entrando no nó. Então:
Pela primeira Lei de Kirchhoff:
Passo 3
Nosso próximo passo será usar as equações características de cada componente.
Para um capacitor é válida a relação:
Então
A queda de tensão em um resistor é dada pela relação:
Portanto
E
Para um indutor a queda é tensão pode ser escrita por:
Pela lei de Kirchhoff vimos que:
E
Como
Chegamos em:
Pela segunda Lei de Kirchhoff:
Pela equação do capacitor:
Pela equação do resistor:
E também vimos que
Então:
E
Resposta
Ei, a resposta está no passo a passo :)