Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.1 - Ex. 23
Considere dois tanques interligados de maneira análoga aos da figura a seguir. O tanque 1 contém, inicialmente, 60 gal de água e oz de sal, enquanto o tanque 2 contém, inicialmente, 100 gal de água e oz de sal. Está entrando no tanque 1, a uma taxa de 3 gal/min, uma mistura de água contendo oz/gal. A mistura no tanque 1 sai a uma taxa de 4 gal/min, da qual metade entra no tanque 2, enquanto o restante deixa o sistema. O tanque 2 recebe de fora uma mistura de água com oz/gal de sal a uma taxa de 1 gal/min. A mistura no tanque 2 sai a uma taxa de 3 gal/min, mas uma parte disso volta para o tanque 1 a uma taxa de 1 gal/min, enquanto o restante deixa o sistema.
(a) Desenhe um diagrama que ilustre o processo de fluxo descrito acima. Sejam e , respectivamente, as quantidades de sal em cada tanque no instante . Escreva as equações diferenciais e as condições iniciais para e que modelam o fluxo.
(b) Encontre os valores de equilíbrio e em função das concentrações e .
(c) É possível (ajustando e ) obter e como um estado de equilíbrio?
(d) Descreva os estados de equilíbrio possíveis para esse sistema para diversos valores de e .
Passo 1
Temos dois tanques com quantidades de sal e . Os dois tanques são abastecidos continuamente e os dois tanques trocam vazões entre si. Sabendo disso, o exercício nos pede para esquematizar o sistema e encontrar a quantidade de sal em cada tanque ao longo do tempo. Vamos lá???
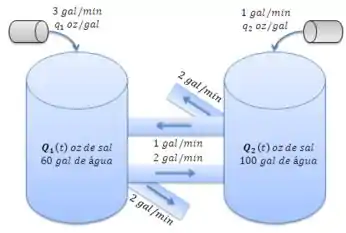
Agora que já temos um desenho do sistema vamos encontrar as equações para as quantidades de sal em cada tanque. Vamos começar delimitando um volume de controle em torno do tanque 1:
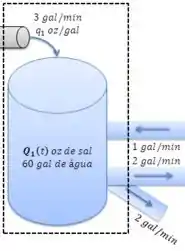
Vamos começar calculando a taxa de sal que entra pelo duto. Temos uma mistura de concentração oz/gal de sal entrando a uma taxa de 3 gal/min.
Então:
Água é retirada do tanque 1 a uma vazão de 4 gal/min, a uma concentração de . Além disso, o tanque 1 recebe uma vazão de 1 gal/min do tanque 2, com uma concentração . O balanço de massa de sal para o tanque 1 fica:
Vamos agora realizar o mesmo procedimento para o tanque 2:
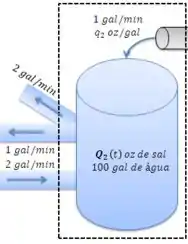
Vamos começar calculando a taxa de sal que entra pelo duto. Temos uma mistura de concentração oz/gal de sal entrando a uma taxa de 1 gal/min.
Então:
O tanque 2 perde água a uma vazão de 3 gal/min, a uma concentração de . Além disso, o tanque 2 recebe uma vazão de 2 gal/min do tanque 1, com uma concentração . O balanço de massa de sal para o tanque 2 fica:
Passo 2
Nosso próximo passo será determinar as concentrações de equilíbrio. No equilíbrio, as concentrações de sal não variam com o tempo, ou seja, e . Ficamos então com:
Somando as duas equações:
Substituindo este resultado:
Passo 3
O próximo passo será verificar se é possível obter e . Substituindo estes valores nas relações que encontramos:
Subtraindo a primeira da segunda equação:
Como é a concentração de sal na mistura é impossível que esta seja negativa. Então é impossível obter estas concentrações de equilíbrio.
Precisamos ainda definir os estados de equilíbrio possíveis. Para isso, vamos começar pelo sistema de equações:
A concentração deve ser positiva. Então:
Vamos agora resolver para :
Subtraindo a primeira da segunda equação:
A concentração deve ser positiva. Então:
Então, as concentrações de equilíbrio devem seguir a relação:
Resposta
Ei, a resposta está no passo a passo :)