Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.1 - Ex. 17

As equações:

m 1 d 2 x 1 d t 2 = k 2 x 2 - x 1 - k 1 x 1 + F 1 t ;

m 2 d 2 x 2 d t 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 t

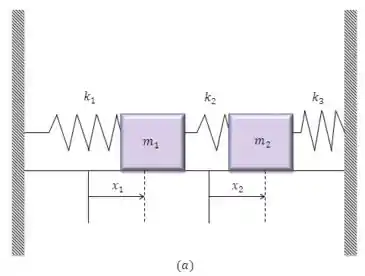
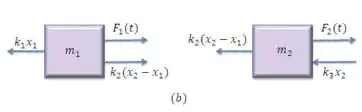
Podem ser deduzidas desenhando-se um diagrama de forças agindo sobre cada massa. A figura (a) mostra a situação quando os dois deslocamentos x 1 e x 2 das duas massas são ambos positivos (para a direita), e x 2 > x 1 . Nesse caso, as molas 1 e 2 estão alongadas, e a mola 3 está comprimida, gerando as forças ilustradas na figura (b). Use a lei de Newton ( F = m a ) para deduzir as equações.

Passo 1

Vamos começar escrevendo as forças que estão agindo sobre cada corpo. O bloco m 1 sofre ação da força F 1 ( t ) e da força elástica da mola 2 para a direita, além da força elástica da mola 1 para a esquerda. Para o bloco 2 temos as forças elásticas das molas 2 e 3 para a esquerda e a força F 2 ( t ) para a direita.

Além disso, a força resultante sobre um corpo é dada por:

F R = ∑ F i

Passo 2

Vamos começar escrevendo a equação de força resultante para o bloco 1:

F R 1 = - k 1 x 1 + k 2 x 2 - x 1 + F 1 ( t )

Analogamente, para o bloco 2:

F R 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 ( t )

Agora que temos as forças resultantes vamos aplicar a segunda lei de Newton para substituir a força resultante. Vamos lá???

Passo 3

Para o bloco 1:

F R 1 = - k 1 x 1 + k 2 x 2 - x 1 + F 1 ( t )

m 1 a 1 = - k 1 x 1 + k 2 x 2 - x 1 + F 1 ( t )

Para o bloco 2:

F R 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 ( t )

m 2 a 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 ( t )

A aceleração pode ser escrita como

a = d V / d t

E, a velocidade é dada por:

V = d x / d t

Então:

a = d V d t = d d t d x d t

a = d 2 x d t 2

Substituindo a aceleração para cada bloco:

m 1 a 1 = m 1 d 2 x 1 d t 2 = - k 1 x 1 + k 2 x 2 - x 1 + F 1 ( t )

E

m 2 a 2 = m 2 d 2 x 2 d t 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 ( t )

E chegamos às mesmas equações do enunciado.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Transforme o sistema: m 1 d 2 x 1 d t 2 = k 2 x 2 - x 1 - k 1 x 1 + F 1 t ; m 2 d 2 x 2 d t 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 t Em um sistema de primeira ordem fazendo y 1 = x 1 , y 2 = x 2 , y 3 =
Considere o circuito ilustrado na figura a seguir.Sejam I 1 , I 2 e I 3 as correntes atravessando, respectivamente, o capacitor, a resistência e o indutor. Analogamente, sejam V 1 , V 2 e V 3 as difer
Considere o circuito ilustrado na figura a seguir. Use o método esboçado no problema 19 para mostrar que a corrente I através do indutor e a diferença de tensão V através do capacitor satisfazem o sis
Considere dois tanques interligados de maneira análoga aos da figura a seguir. O tanque 1 contém, inicialmente, 60 gal de água e Q 1 0 oz de sal, enquanto o tanque 2 contém, inicialmente, 100 gal de á
Considere os dois tanques interligados na figura a seguir. O tanque 1 contém, inicialmente, 30 gal de água e 25 oz de sal, enquanto o tanque 2 contém, inicialmente, 20 gal de água e 15 oz de sal. Entr