Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.1 - Ex. 22
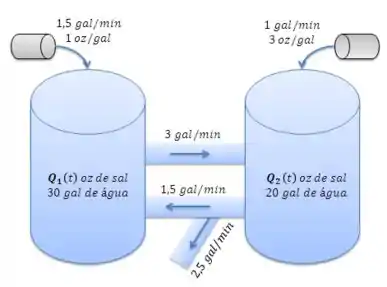
Considere os dois tanques interligados na figura a seguir. O tanque 1 contém, inicialmente, 30 gal de água e 25 oz de sal, enquanto o tanque 2 contém, inicialmente, 20 gal de água e 15 oz de sal. Entra no tanque 1 uma mistura de água contendo 1 oz/gal de sal a uma taxa de 1,5 gal/min. A mistura flui do tanque 1 para o tanque 2 a uma taxa de 3 gal/min. Entra também, no tanque 2 (vindo de fora) uma mistura de água contendo 3 oz/gal de sal a uma taxa de 1 gal/min. A mistura escorre do tanque 2 a uma taxa de 4 gal/min e parte dela volta para o tanque 1 a uma taxa de 1,5 gal/min, enquanto o restante deixa o sistema.
(a) Sejam e , respectivamente, as quantidades de sal em cada tanque no instante . Escreva as equações diferenciais e as condições iniciais que modelam o processo de fluxo. Observe que o sistema de equações diferenciais é não homogêneo.
(b) Encontre os valores de e para os quais o sistema está em equilíbrio, ou seja, não varia com o tempo. Sejam e os valores de equilíbrio. Você pode prever qual tanque atingirá seu estado de equilíbrio mais rapidamente?
(c) Sejam e . Determine um problema de valor inicial para e . Observe que o sistema de equações para e é homogêneo.
Passo 1
Temos dois tanques com quantidades de sal e . Os dois tanques são abastecidos continuamente e os dois tanques trocam vazões entre si. Sabendo disso, o exercício nos pede para encontrar a quantidade de sal em cada tanque ao longo do tempo. Vamos lá???
Nosso primeiro passo será estabelecer um volume de controle ao redor do tanque 1:
Vamos começar calculando a taxa de sal que entra pelo duto. Temos uma mistura de concentração 1 oz/gal de sal entrando a uma taxa de 1,5 gal/min.
Então:
O tanque 1 transmite uma vazão de água de 3 gal/min para o tanque 2, a uma concentração de . Analogamente, o tanque 1 recebe uma vazão de 1,5 gal/min do tanque 2, com uma concentração . O balanço de massa de sal para o tanque 1 fica:
Vamos agora realizar o mesmo procedimento para o tanque 2:
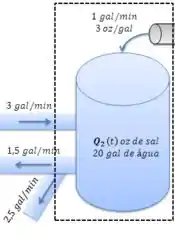
Vamos começar calculando a taxa de sal que entra pelo duto. Temos uma mistura de concentração 3 oz/gal de sal entrando a uma taxa de 1 gal/min.
Então:
O tanque 2 perde água a uma vazão de 4 gal/min, a uma concentração de . Além disso, o tanque 2 recebe uma vazão de 3 gal/min do tanque 1, com uma concentração . O balanço de massa de sal para o tanque 2 fica:
Passo 2
O item (b) nos pede para encontrar as concentrações de sal de equilíbrio. No equilíbrio, as concentrações de sal não variam com o tempo, ou seja, e . Ficamos então com:
Somando as equações:
Então:
Como os dois tanques estão interligados é esperado que o equilíbrio só seja atingido quando os dois tanques chegarem ao estado de equilíbrio. Assim, o sistema só entra em equilíbrio se os dois tanques atingirem a concentração de equilíbrio.
Passo 3
Devemos agora aplicar as funções e no sistema de equações diferenciais e verificar que chegaremos a um sistema homogêneo. Vamos lá?
Voltando para o sistema que encontramos:
Vamos chamá-lo de sistema (I). Se aplicarmos a condição de equilíbrio e ficaremos com:
Vamos chamá-lo de sistema (II).
Se fizermos agora sistema (I)-sistema (II):
Rearranjando:
Portanto, provamos que a substituição por e gera um sistema homogêneo.
Nosso último passo é definir as condições de valor inicial.
Resposta
Ei, a resposta está no passo a passo :)