Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.1 - Ex. 12
12.Um ponto P no primeiro quadrante está no gráfico da função . Expresse as coordenadas de P em função do coeficiente angular da reta que liga P à origem.
Passo 1
Show, olha só galera. Como , pra escrever as coordenadas do ponto em função de é tranquilo:
Mas não queremos exatamente em função de e sim em função do coeficiente angular da reta que liga o ponto a origem:
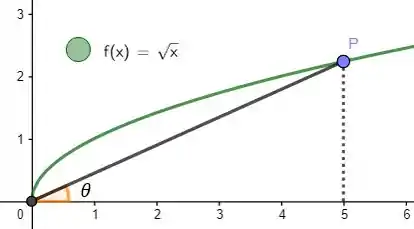
Mãos a obra então.
Passo 2
Vamos chamar esse coeficiente angular de . Pra qualquer reta, esse coeficiente nada mais é do que:
E veja só, a altura do ponto nada mais é do que , bem como a base do triângulo o valor de correspondente! Sendo assim:
Dái tiramos:
Como as coordenadas do ponto são:
Pra escrever em função da inclinação basta substituir:
Resposta
Exercícios de Livros Relacionados
3. Um copo cheio de agua a uma temperatura de 11 ° C é colocado em uma sala que está á temperatura constante de 21 ° C . Faça um gráfico aproximado que descreva razoavelmente a temperatura da agua no
8. Denote por C o gráfico de y = 1 / x , para x0 .Expresse a distância entre o ponto P ( 1 ,0 ) e um ponto Q de C como uma função coordenada de x de Q .Qual é o dominio da função distância obtida em (
4. Suponha que queiramos pintar a tampa de uma mesa circular. Encontre uma fórmula que expresse a quantidade de tinta necessária como uma função do raio da tampa e discuta todas as hipóteses utilizada
7. Uma caixa fechada deve ser feita de um pedaço de papelão com 180cm por 300 cm, tirando fora quatro quadrados de mesmo tamanho (veja a figura abaixo), dobrando ao longo das retas tracejadas e encaix
5. Um contêiner de base quadrada e lados retangulares sem tampa tem um volume de 8 metros cúbicos. O material da base custa $ 5 por metro quadrado e o lados, $ 2 por metro quadrado.Encontre uma fórmul