Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.4 - Ex. 11d
Considere o sistema (3) no Exemplo 1 do texto. Lembre-se de que esse sistema tem um ponto critico assinoticamente estavel em (0,5; 0,5), correspondente a coexistência estável das populações das duas espécies. Suponha, agora, que a imigração ou emigração ocorrem com taxas constantes δa e δb para as espécies x e y, respectivamente. Nesse caso, as Eqs. (3) são substituídas por
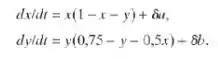
O problema é saber qual efeito disto na localização do ponto de equilíbrio estável.
Suponha que a > 0 e b > 0, de modo que a imigração ocorre para ambas as espécies. Mostre que a solução de equilíbrio resultante pode representar um aumento nas duas populações, ou um acréscimo em uma e um decréscimo em outra. Explique, intuitivamente, por que esse é um resultado razoável.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos os valores críticos das equações e achar o equilíbrio. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser determinar quais os pontos críticos, ou seja, igualar as derivadas a zero.
Os termos que nos levam à linearidade do sistema são multiplicados por delta, ou seja:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Substituindo
Se tiverrmos a > b, a população 1 vai crescer, e vice-versa. Se 2b > a, a população da espécie 2 vai crescer, e vice-versa.
Resposta
Se tiverrmos a > b, a população 1 vai crescer, e vice-versa. Se 2b > a, a população da espécie 2 vai crescer, e vice-versa.