Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 1

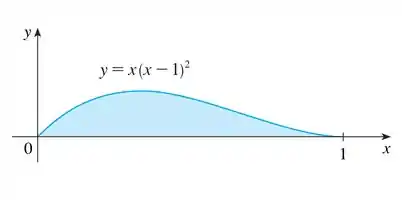
Considere s o solido obtido pela rotação da região mostrada na figura em torno no do eixo y . Explique por que é complicado usar fatias para encontrar o volume V de S. Esboce uma casca de aproximação típica. Quais são a circunferência e altura ? Use cascas para encontrar V.

Passo 1

Opa! Bora resolver esse problema! Temos a seguinte curva:

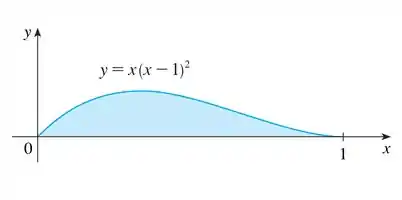
A partir da rotação dessa região em torno do eixo y obtemos um sólido s . O enunciado pede pra a gente explicar por que é complicado usar fatias para encontrar o volume V de S .

Se usássemos o método 'anelar', primeiro teríamos de localizar o ponto máximo local ( a , b ) de y = x x - 1 2 usando os métodos do capítulo 4. Então teríamos que resolver a equação:

y = x x - 1 2

Para x na em termos de y para obter as funções x = g 1 ( x ) e x = g 2 ( x ) mostradas na na figura:

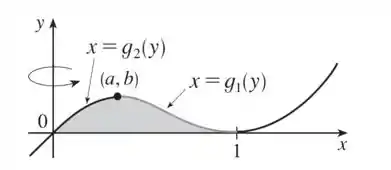
Essa etapa seria difícil porque envolve a fórmula cúbica. Finalmente, reduziríamos o volume usando:

V =     ∫ 0 b   [ g 1 y 2 - g 2 y 2 }   d y  

Passo 2

Usando o método das conchas, descobrimos que uma casca típica aproximada tem raio x , então sua circunferência é 2 π x   .   Assim:

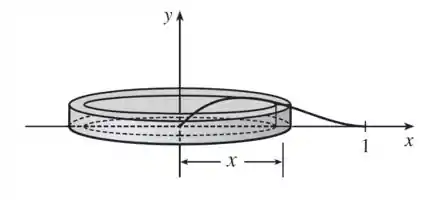
Sua altura é y , ou seja, x x - 1 2 . Então o volume total é :

V = ∫ 0 1   2 π x   x x - 1 2 d x

V = 2 π ∫ 0 1   x 4 - 2 x 3 + x 2 d x

Integrando temos:

V = 2 π x 5 5 - 2 x 4 4 + x 3 3 0 1 = π 15

Prontinho!

Resposta

V = 2 π x 5 5 - 2 x 4 4 + x 3 3 0 1 = π 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que você faça anéis para guardanapos perfurando buracos com diferentes diâmetros através de duas bolas de madeira (as quais têm diferentes diâmetros). Você descobre que ambos os anéis de guard
Use o método das cascas cilíndricas para encontrar o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno do eixo x.
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x ² , y = 0 ,