Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 64
Seem qual intervalo é crescente?
Passo 1
Oie!
Temos que encontrar em qual intervalo a seguinte função é crescente:
Já que temos que saber onde é crescente, precisamos encontrar a derivada, concorda?
E a função é crescente onde a derivada é positiva. Então é isso que vamos analisar.
Para isso vamos usar o Teorema fundamental do cálculo.
O teorema diz que se você primeiro integra uma função contínua e depois diferencia o resultado (ou vice-versa), você volta à função original. É tipo um passe de mágica matemático! ✨
O TFC (teorema fundamental do cálculo), que nos diz:
Onde e , são as integrais da função, onde substituímos as variáveis pelos limites da integral.
Ou seja, a derivada que estamos procurando é a mesma função que está dentro da integral, avaliada para os limites da integral!
Bora lá!
Passo 2
Vamos identificar a nossa derivada, temos:
A gente consegue esse resultado usando o Teorema Fundamental do Cálculo. Ele basicamente diz que, se você tem uma integral com um limite variável, a derivada dessa integral é só a função que está dentro da integral, avaliada no limite superior. Bem simples, né? É tipo dizer que a derivada da integral é a própria função dentro dela, só que aplicada no ponto onde a integração termina. Fácil assim!
Passo 3
Como precisamos que a função seja crescente, precisamos que
Ou seja,
Isso significa que temos duas situações:
- e
- e
Mas, veja, a exponencial é sempre positiva, então a situação II nunca irá acontecer. Daí, de I),
Em outras palavras,
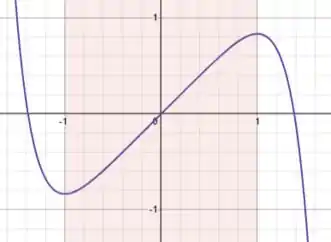
Repare que é exatamente a parte colorida do gráfico, onde varia de a , que a função é crescente