Consideremos o problema de projetar uma linha férrea de modo a fazer transições lisas entre as seções de trilhos restos. Um trilho existente aod longo daparte negativa do eixo precisa ser ligado a um trilho que corre ao longo da reta para .
- Determine um polinômio de grau tal que a função definida por
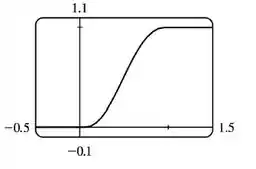
- Utilize uma calculadora gráfica ou um computador para traçar o gráfico de .
seja continua e tenha derivada e curvatura conínuas.
Passo 1
- Vamos lá, para a função ser contínua temos que ter e e para ser contínua temos que ter .
- Utilizando uma calculadora gráfica vamos obter o gráfico de abaixo:
A curvatura da curva no ponto é:
E por ultimo para ser contínua temos que ter .
Passo 2
Vamos então escrever como um polinômio de grau :
Agora vamos achar e :
Passo 3
Vamos agora usar as seis condições que temos:
Já achamos que , vamos resolver o sistema com as três equações que sobraram:
Multiplicando a segunda expressão por e somando com a terceira, e multiplicando a primeira por e subtraindo da segunda ficamos com:
Pronto, temos todos o valores, agora é só substituir em :
Passo 4

Resposta