Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 51

Determine as equações para o círculo osculador da elipse 9 x 2 + 4 y 2 = 36 nos pontos ( 2,0 ) e ( 0,3 ) . Utilize uma calculadora gráfica ou computador para traçar a elipse e ambos os círculos osculadores na mesma tela.

Passo 1

Olá, meu amigo. Aqui deveremos encontrar as equações para o círculo osculador da elipse:

9 x 2 + 4 y 2 = 36

Nos pontos:

2,0

E

0,3

O círculo osculador, também conhecido como círculo de curvatura, é um conceito em geometria diferencial que descreve o círculo que mais se aproxima de uma curva em um ponto específico. Este círculo tem o mesmo raio de curvatura que a curva nesse ponto e é tangente à curva.

A circunferência osculadora no ponto toca o gráfico e tem raio ( 1 κ = κ - 1 ) .

A circunferência osculadora está sempre situada no lado côncavo inferior do gráfico.

Observe que o centro da circunferência osculadora está localizado na normal à curva nesse ponto.

Para que possarmos dar início a resolução, precisamos colocar a equação da elipse que está no formato:

9 x 2 + 4 y 2 = 36

No formato que a gente já conhece.

Agora temos que uma parametrização para a elipse:

x 2 a 2 + y 2 b 2 = 1

r t = a cos ⁡ t ,   b sin ⁡ t ,   0

Então para a nossa elipse:

r t = ( 2 cos ⁡ t , 3 sen ⁡ t , 0 )

E para acharmos a curvatura k dela, iremos utilizar da fórmula:

κ = | r ' × r ' ' | r ' 3

Passo 2

Temos então que a nossa elipse tem a equação:

9 x 2 + 4 y 2 = 36

Veja que se dividirmos todos os membros por 36 :

x 2 4 + y 2 9 = 1

Para isso, vamos calcular as derivadas:

r t = ( 2 cos ⁡ t , 3 sen ⁡ t , 0 )

r ' = ( - 2 sen ⁡ t , 3 cos ⁡ t , 0 )

r ' ' = ( - 2 cos ⁡ t , - 3 sen ⁡ t , 0 )

Calculando o produto vetorial utilizamos a ‘fórmula’:

r ' × r ' ' = i j k r x ' r y ' r z ' r x ' ' r y ' ' r z ' '

Substituindo:

r ' × r ' ' = i j k - 2 sen ⁡ t 3 cos ⁡ t 0 - 2 cos ⁡ t - 3 sen ⁡ t 0

Calculando o determinante levando em consideração os produtos vetoriais entre os versores:

r ' × r ' ' = 0,0 , 6 sen 2 ⁡ t + 6 cos 2 ⁡ t

r ' × r ' ' = 0,0 , 6

Calculando o módulo agora

r ' × r ' ' = 0 + 0 + 6 2 = 6

Calculando agora o módulo da primeira derivada

r ' = - 2 sen ⁡ t 2 + 3 cos ⁡ t 2 + 0

r ' = 4 sen 2 ⁡ t + 9 cos 2 ⁡ t

Passo 3

A curvatura então é

κ = | r ' × r ' ' | r ' 3

κ = 6 4 sen 2 ⁡ t + 9 cos 2 ⁡ t 3 / 2

Nos pontos ( 2,0 ) e ( 0,3 ) , temos t = 0 e t = π / 2

κ 0 = 6 9 3 / 2 = 6 3 3 = 2 3 2 = 2 9

κ π 2 = 6 4 3 / 2 = 6 2 3 = 3 2 2 = 3 4

Passo 4

Analisando o gráfico da elipse

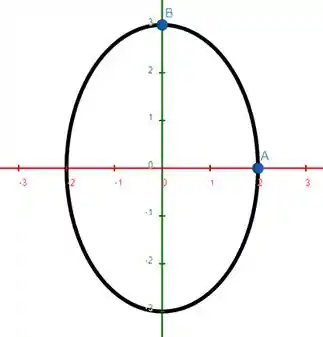
No ponto A = ( 2,0 ) o vetor normal vai para a direita horizontalmente, então precisamos de uma circunferência com raio r = 9 / 2   que contenha o ponto A e o y do centro é 0 . Então a circunferência tem a forma

x - x 0 2 + y 2 = 81 4

Para conter o ponto A , temos que descobrir x 0 , substituindo o ponto na equação:

2 - x 0 2 + 0 2 = 81 4

Realizando o produto notável:

4 - 4 x 0 + x 0 2 = 81 4

Passando todo mundo para o lado esquerdo da igualdade:

x 0 2 - 4 x 0 + 4 - 81 4 = 0

Simplificando:

x 0 2 - 4 x 0 - 65 4 = 0

Calculando x 0 por Bhaskara

Δ = - 4 2 - 4 ⋅ 1 ⋅ - 65 4

Δ = 16 + 65 = 81

x 0 = - - 4 ± 9 2

Se pegarmos a raiz positiva, a circunferência fica do lado de fora da elipse, então

x 0 = - 5 2

Então nossa circunferência osculadora a função no ponto ( 2,0 ) é

x + 5 2 2 + y 2 = 81 4

Passo 5

No ponto A = ( 0,3 ) o vetor normal vai para cima verticalmente, então precisamos de uma circunferência com raio r = 4 / 3   que contenha o ponto b e o x do centro é 0 . Então a circunferência tem a forma

x 2 + ( y - y 0 ) 2 = 16 9

Para conter o ponto B , temos que descobrir y 0 , substituindo o ponto na equação

0 2 + ( 3 - y 0 ) 2 = 16 9

y 0 2 - 6 y 0 + 9 = 16 9

y 0 2 - 6 y 0 + 65 9 = 0

Calculando y 0 por Bhaskara

Δ = - 6 2 - 4 ⋅ 1 ⋅ 65 9

Δ = 36 - 260 9 = 64 9

y 0 = - - 6 ± 8 3 2

Se pegarmos a raiz positiva, a circunferência fica do lado de fora da elipse, então

y 0 = 10 3 2 = 10 6 = 5 3

Então nossa circunferência osculadora a função no ponto ( 0,3 ) é

x 2 + y - 5 3 2 = 16 9

Passo 6

No gráfico temos então a nossa elipse e os seus círculos:

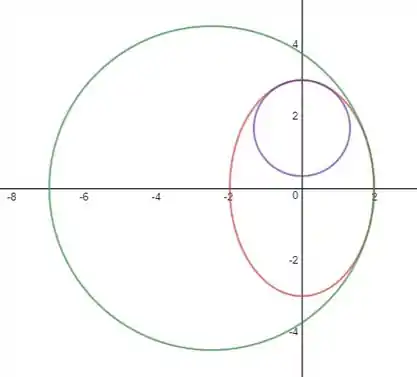
Resposta

No ponto ( 2,0 ) :

x + 5 2 2 + y 2 = 81 4

No ponto ( 0,3 ) :

x 2 + y - 5 3 2 = 16 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t = cos ⁡ ti - cos ⁡ t j + sin ⁡ t k
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce. r t =1 + t , 3 t ,- t
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = e - tcos ⁡ t y = e - t sin ⁡ tz = e - t ( 1,0 , 1 )
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = ln ⁡ ty = 2 t z = t 2 ; ( 0,2 , 1 )
Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. x = t 5 y = t 4 z = t 3 ( 1,1 , 1 )