Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 5
As coordenadas cartesianas de um ponto são dadas.
(i) Encontre as coordenadas polares do ponto, onde e .
(ii) Encontre as coordenadas polares do ponto, onde e .
a) b)
Passo 1
Olá, meu nobre estudante. Vou te ajudar a resolver mais uma atividade hoje.
O problema fornece as coordenadas de dois pontos em coordenadas cartesianas
e pede para acharmos as coordenadas polares!
Para isso, lembre-se que para isso, vamos utilizar a relação entre coordenadas polares e cartesianas.
Assim o que a gente vai fazer é encontrar o valor de e depois utilizar na equação de e para que possamos encontrar o ângulo
Passo 2
Assim, para o primeiro ponto,
Portanto,
O ângulo deve estar no primeiro quadrante:
Logo, as coordenadas polares desse ponto são
Para descrever esse ponto com , basta somar no ângulo, isso ficar melhor visualizado no ciclo trigonométrico abaixo:
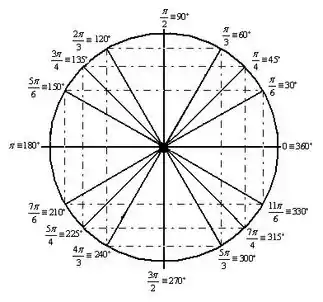
Passo 3
Basta fazer o mesmo com o segundo ponto:
Assim,
Portanto, vemos que o ângulo está no quarto quadrante:
Para , se somarmos obteremos . Assim, nesse caso vamos subtrair , ou você pode olhar nesse círculo trigonométrico com os valores de seno e cosseno e seus ângulos, que se com estamos em , para chegarmos a , o oposto, é só seguirmos a direção oposta do ponto no círculo trigonométrico, que é o
